Исследование операций
ГЛАВА 1
ПРЕДМЕТ И ЗАДАЧИ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ
§ 1. Что такое исследование операций и чем оно занимается
В наше время, которое по справедливости называют эпохой научно-технической революции, наука уделяет все большее внимание вопросам организации и управления. Причин этому много. Быстрое развитие и усложнение техники, небывалое расширение масштабов проводимых мероприятий и спектра их возможных последствий, внедрение автоматизированных систем управления (АСУ) во все области практики — все это приводит к необходимости анализа сложных целенаправленных процессов под углом зрения их структуры и организации. От науки требуются рекомендации по оптимальному (разумному) управлению такими процессами. Прошли времена, когда правильное, эффективное управление находилось организаторами «на ощупь», методом «проб и ошибок». Сегодня для выработки такого управления требуется научный подход — слишком велики потери, связанные с ошибками.
Потребности практики вызвали к жизни специальные научные методы, которые удобно объединять под названием «исследование операций». Под этим термином мы будем понимать применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности.
Поясним, что понимается под «решением». Пусть предпринимается какое-то мероприятие, направленное к достижению определенной цели. У лица (или группы лиц), организующего мероприятие, всегда имеется какая-то свобода выбора: оно может организовать его тем или другим способом, например, выбрать образцы техники, которые будут применены, так или иначе распределить имеющиеся средства и т. д. «Решение» это и есть какой-то выбор из ряда возможностей, имеющихся у организатора. Решения бывают плохими
и хорошими, продуманными и скороспелыми, обоснованными и произвольными.
Необходимость принятия решений так же стара, как само человечество. Несомненно, уже в доисторические времена первобытные люди, отправляясь, скажем, охотиться на мамонта, должны были принимать те или другие решения: в каком месте устроить засаду? Как расставить охотников? Чем их вооружить? и т.
д. Мы с вами в повседневной жизни, сами того не замечая, на каждом шагу принимаем решения. Например, выходя утром из дому, чтобы идти на работу, мы должны принять целый ряд решений: как одеться? Брать ли с собой зонтик? В каком месте перейти улицу? Каким видом транспорта воспользоваться? и т. д. Руководитель предприятия тоже должен постоянно принимать решения типа: как распорядиться имеющейся рабочей силой? Какие типы работ выполнить в первую очередь? и т. д.
Значит ли это, что, принимая подобные решения, мы занимаемся «исследованием операций»? Нет, не значит. Исследование операций начинается тогда, когда для обоснования решений применяется тот или другой математический аппарат. До поры до времени решения в любой области практики принимаются без специальных математических расчетов, просто на основе опыта и здравого смысла. Скажем, для решения вопроса о том, как одеться, выходя на улицу, и где ее перейти, математика не нужна, да и вряд ли потребуется в дальнейшем. Оптимизация таких решений происходит как бы сама собой, в процессе жизненной практики. Если порой принятое решение окажется не самым удачным, так что же? На ошибках учатся!
Однако бывают решения куда более ответственные. Пусть, например, организуется работа общественного транспорта в новом городе с сетью предприятий, жилыми массивами и т. д. Необходимо принять ряд решений: по каким маршрутам и какие транспортные средства направить? В каких пунктах сделать остановки? Как изменять частоту следования машин в зависимости от времени суток? и т. д.
Эти решения — гораздо сложнее, а главное, от них очень многое зависит. Неправильный их выбор может отразиться на деловой жизни целого города. Конечно, и в этом случае при выборе решения можно действовать интуитивно, опираясь на опыт и здравый смысл (так оно нередко и делается). Но гораздо разумнее будут решения, если они подкреплены математическими расчетами. Эти предварительные расчеты помогут избежать длительного и дорогостоящего поиска нужного решения «на ощупь».
Возьмем еще более яркий пример. Пусть речь идет о каком-то очень крупномасштабном мероприятии — скажем, об отведении части стока северных рек в засушливые зоны. Допустимо ли здесь произвольное, «волевое» решение, могущее привести к серьезным отрицательным последствиям, или же необходима серия предварительных расчетов по математическим моделям? Думается, что здесь двух мнений быть не может — необходимость тщательных, многосторонних расчетов очевидна.
«Семь раз примерь, один — отрежь», — говорит пословица. Исследование операций как раз и есть своеобразное математическое «примеривание» будущих решений, позволяющее экономить время, силы и материальные средства, избегать серьезных ошибок, на которых уже нельзя «учиться» (слишком дорого это обходится).
Чем сложнее, дороже, масштабнее планируемое мероприятие, тем менее допустимы в нем «волевые» решения и тем важнее становятся научные методы, позволяющие заранее оценить последствия каждого решения, заранее отбросить недопустимые варианты и рекомендовать наиболее удачные; установить, достаточна ли имеющаяся у нас информация для правильного выбора решения, и если нет — какую информацию нужно получить дополнительно. Слишком опасно в таких случаях опираться па свою интуицию, на «опыт и здравый смысл». В нашу эпоху научно-технической революции техника и технология меняются настолько быстро, что «опыт» просто не успевает накапливаться. К тому же часто идет речь о мероприятиях уникальных, проводимых впервые. «Опыт» в этом случае молчит, а «здравый смысл» легко может обмануть, если не опирается на расчет. Такими расчетами, облегчающими людям принятие решений, и занимается исследование операций.
Как уже говорилось, это — сравнительно молодая наука (хотя понятие «молодости» в научном мире относительно; многие, едва возникшие науки «истлевают на корню», так и не найдя приложений). Впервые название «исследование операций» появилось в годы второй мировой войны, когда в вооруженных силах некоторых стран (США, Англии) были сформированы специальные группы научных работников (физиков, математиков, инженеров), в задачу которых входила подготовка проектов решений для командующих боевыми действиями.
Эти решения касались главным образом боевого применения оружия и распределения сил и средств по различным объектам. Подобного рода задачами (правда, под иными названиями) занимались и ранее, в частности, в нашей стране. В дальнейшем исследование операций расширило область своих применений на самые разные области практики: промышленность, сельское хозяйство, строительство, торговля, бытовое обслуживание, транспорт, связь, здравоохранение, охрана природы и т. д. Сегодня трудно назвать такую область практики, где бы не применялись, в том или другом виде, математические модели и методы исследования операций.
Чтобы познакомиться со спецификой этой науки, рассмотрим ряд типичных для нее задач. Эти задачи, намеренно взятые из самых разных областей практики, несмотря на некоторую упрощенность постановки, дают все же понятие о том, каков предмет и каковы цели исследования операций.
1. План снабжения предприятий. Имеется ряд предприятий, потребляющих известные виды сырья, и есть ряд сырьевых баз, которые могут поставлять это сырье предприятиям. Базы связаны с предприятиями какими-то путями сообщения (железнодорожными, водными, автомобильными, воздушными) со своими тарифами. Требуется разработать такой план снабжения предприятий сырьем (с какой базы, в каком количестве и какое сырье доставляется), чтобы потребности в сырье были обеспечены при минимальных расходах на перевозки.
2. Постройка участка магистрали. Сооружается участок железнодорожной магистрали. В нашем распоряжении — определенное количество средств: людей,. строительных машин, ремонтных мастерских, грузовых автомобилей и т. д. Требуется спланировать строительство (т. е. назначить очередность работ, распределить машины и людей по участкам пути, обеспечить ремонтные работы) так, чтобы оно было завершено в минимально возможный срок.
3. Продажа сезонных товаров. Для реализации определенной массы сезонных товаров создается сеть временных торговых точек. Требуется выбрать разумным образом: число точек, их размещение, товарные запасы и количество персонала па каждой из них так, чтобы обеспечить максимальную экономическую эффективность распродажи.
4. Снегозащита дорог. В условиях Крайнего Севера метели, заносящие снегом дороги, представляют серьезную помеху движению. Любой перерыв движения приводит к экономическим потерям. Существует ряд возможных способов снегозащиты (профиль дороги, защитные щиты и т. д.), каждый из которых требует известных затрат на сооружение и эксплуатацию. Известны господствующие направления ветров, есть данные о частоте и интенсивности снегопадов. Требуется разработать наиболее эффективные экономически средства снегозащиты (какую из дорог, как и чем, защищать?) с учетом потерь, связанных с заносами.
5. Противолодочный рейд. Известно, что в некотором районе морского театра военных действий находится подводная лодка противника. Группа самолетов противолодочной обороны получила задание: разыскать, обнаружить и уничтожить лодку. Требуется рационально организовать операцию (рейд): выбрать маршруты самолетов, высоту полета, способ атаки так, чтобы с максимальной уверенностью обеспечить выполнение боевого задания.
6. Выборочный контроль продукции. Завод выпускает определенного вида изделия. Для обеспечения их высокого качества организуется система выборочного контроля. Требуется разумно организовать контроль (т. е. выбрать размер контрольной партии, набор тестов, правила браковки и т. д.) так, чтобы обеспечить заданный уровень качества при минимальных расходах на контроль.
7. Медицинское обследование. Известно, что в каком-то районе обнаружены случаи опасного заболевания. С целью выявления заболевших (или носителей инфекции) организуется медицинское обследование жителей района. На это выделены материальные средства, оборудование, медицинский персонал. Требуется разработать такой план обследования (число медпунктов, их размещение, последовательность осмотров специалистами, виды анализов и т. д.), который позволит выявить, по возможности, максимальный процент заболевших и носителей инфекции.
8. Библиотечное обслуживание. Крупная библиотека обслуживает запросы, поступающие от абонентов. В фондах библиотеки имеются книги, пользующиеся повышенным спросом, книги, на которые требования поступают реже и, наконец, книги, почти никогда не запрашиваемые.
Имеется ряд возможностей распределения книг по стеллажам и хранилищам, а также по диспетчеризации запросов с обращениями в другие библиотеки. Нужно разработать такую систему библиотечного обслуживания, при которой запросы абонентов удовлетворяются в максимальной мере.
Число примеров легко было бы умножить, но и приведенных достаточно, чтобы представить себе характерные особенности задач исследования операций. Хотя примеры относятся к самым различным областям, в них легко просматриваются общие черты. В каждом из них речь идет о каком-то мероприятии, преследующем определенную цель. Заданы некоторые условия, характеризующие обстановку (в частности, средства, которыми мы можем распоряжаться). В рамках этих условий требуется принять такое решение, чтобы задуманное мероприятие было в каком-то смысле наиболее выгодным.
В соответствии с этими общими чертами вырабатываются и общие приемы решения подобных задач, в совокупности, составляющие методологическую схему и аппарат исследования операций.
Внимательный читатель, знакомясь с приведенными выше примерами, вероятно, заметил, что не для всех из них на практике применяются математические методы обоснования решений; в некоторых случаях решения принимаются по старинке, на глаз. Однако с течением времени доля задач, где для выбора решения применяются математические методы, постоянно растет. Особенно большую роль приобретают эти методы по мере внедрения АСУ (автоматизированных систем управления) во все области практики. Создание АСУ (если она применяется для управления, а не только для сбора и обработки информации) невозможно без предварительного обследования управляемого процесса методами математическою моделирования. С ростом масштабов и сложности мероприятий математические методы обоснования решений приобретают все большую роль. Работа небольшого аэродрома вполне может быть обеспечена силами одного опытного диспетчера; работа крупного аэропорта требует автоматизированной системы управления, работающей согласно четкому алгоритму.
Выработка такого алгоритма всегда основывается на предварительных расчетах, т. е. на исследовании операций.
§ 2. Основные понятия и принципы исследования операций
В этом параграфе мы познакомимся с терминологией, основными понятиями и принципами науки «исследование операций».
Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению какой-то цели (все мероприятия, рассмотренные в пунктах 1 — 8 предыдущего параграфа, являются «операциями»).
Операция есть всегда управляемое мероприятие, т. е. от нас зависит, каким способом выбрать некоторые параметры, характеризующие её организацию. «Организация» здесь понимается в широком смысле слова, включая набор технических средств, применяемых в операции.
Всякий определенный выбор зависящих от нас параметров называется решением. Решения могут быть удачными и неудачными, разумными и неразумными. Оптимальными называются решения, по тем или другим признакам предпочтительные перед другими. Цель исследования операций — предварительное количественное обоснование оптимальных решений.
Иногда (относительно редко) в результате исследования удается указать одно-единственное строго оптимальное решение, гораздо чаще — выделить область практически равноценных оптимальных (разумных) решений, в пределах которой может быть сделан окончательный выбор.
Заметим, что само принятие решения выходит за рамки исследования операции и относится к компетенции ответственного лица, чаще — группы лиц, которым предоставлено право окончательного выбора и на которых возложена ответственность за этот выбор. Делая выбор, они могут учитывать, наряду с рекомендациями, вытекающими из математического расчета, еще ряд соображений (количественного и качественного характера), которые этим расчетом не были учтены.
Непременное присутствие человека (как окончательной инстанции, принимающей решение) не отменяется даже при наличии полностью автоматизированной системы управления, которая, казалось бы, принимает решение без участия человека.
Нельзя забывать о том, что само создание управляющего алгоритма, выбор одного из возможных его вариантов, есть тоже решение, и весьма ответственное. По мере развития управляющих автоматов функции человека не отменяются, а просто перемещаются с одного, элементарного, уровня на другой, высший. Кроме того, ряд автоматизированных систем управления предусматривает в ходе управляемого процесса активное вмешательство человека.
Те параметры, совокупность которых образует решение, называются элементами решения. В качестве элементов решения могут фигурировать различные числа, векторы, функции, физические признаки и т. д. Например, если составляется план перевозок однородных грузов из пунктов отправления А1,А2,…, Аm в пункты назначения В1,В2, ..., Вn, то элементами решения будут числа xij, показывающие, какое количество груза будет отправлено из 1-го пункта отправления Аi в j-й пункт назначения Вj. Совокупность чисел x11, x12, …, x1n, …, xm1, xm2, …, xmn образует решение.
В простейших задачах исследования операций количество элементов решения может быть сравнительно невелико. Но в большинстве задач, имеющих практическое значение, число элементов решения очень велико, в чем читатель может убедиться, попытавшись самостоятельно выделить и «назвать по имени» элементы решения в примерах 1 — 8 предыдущего параграфа. Для упрощения мы будем всю совокупность элементов решения обозначать одной буквой x и говорить «решение х».
Кроме элементов решения, которыми мы, в каких-то пределах, можем распоряжаться, в любой задаче исследования операций имеются еще и заданные, «дисциплинирующие» условия, которые фиксированы с самого начала и нарушены быть не могут (например, грузоподъемность машины; размер планового задания;
весовые характеристики оборудования и т. п.). В частности, к таким условиям относятся средства (материальные, технические, людские), которыми мы вправо распоряжаться, и иные ограничения, налагаемые на решение. В своей совокупности они формируют так называемое «множество возможных решений».
Обозначим это множество опять-таки одной буквой X, а тот факт, что решение х принадлежит этому множеству, будем записывать в виде формулы: х

(читается: элемент х входит в множество X).
Речь идет о том, чтобы в множестве возможных решений Х выделить те решения х (иногда — одно, а чаще — целую область решений), которые с той или другой точки зрения эффективнее (удачнее, предпочтительнее) других. Чтобы сравнивать между собой по эффективности разные решения, нужно иметь какой-то количественный критерий, так называемый показатель эффективности (его часто называют «целевой функцией»). Этот показатель выбирается так, чтобы он отражал целевую направленность операции. «Лучшим» будет считаться то решение, которое в максимальной степени способствует достижению поставленной цели. Чтобы выбрать, «назвать по имени» показатель эффективности W, нужно, прежде всего, спросить себя: чего мы хотим, к чему стремимся, предпринимая операцию? Выбирая решение, мы, естественно, предпочтем такое, которое обращает показатель эффективности W в максимум (или же в минимум). Например, доход от операции хотелось бы обратить в максимум; если же показателем эффективности являются затраты, их желательно обратить в минимум. Если показатель эффективности желательно максимизировать, мы это будем записывать в виде W => mах, а если минимизировать — W => min.
Очень часто выполнение операции сопровождается действием случайных факторов («капризы» погоды, колебания спроса и предложения, отказы технических устройств и т. д.). В таких случаях обычно в качестве показателя эффективности берется не сама величина, которую хотелось бы максимизировать (минимизировать), а ее среднее значение (математическое ожидание).
В некоторых случаях бывает, что операция, сопровождаемая случайными факторами, преследует какую-то вполне определенную цель А,
которая может быть только достигнута полностью или совсем не достигнута (схема «да—нет»), и никакие промежуточные результаты нас не интересуют. Тогда в качестве показателя эффективности выбирается вероятность достижения этой цели Р(А). Например, если ведется стрельба по какому-то объекту с непременным условием уничтожить его, то показателем эффективности будет вероятность уничтожения объекта.
Неправильный выбор показателя эффективности очень опасен. Операции, организованные под углом зрения неудачно выбранного критерия, могут привести к неоправданным затратам и потерям (вспомним хотя бы пресловутый «вал» в качестве основного критерия оценки хозяйственной деятельности предприятий).
Для иллюстрации принципов выбора показателя эффективности вернемся опять к примерам 1 — 8 § 1, выберем для каждого из них естественный показатель эффективности и укажем, требуется его максимизировать или минимизировать. Разбирая примеры, нужно иметь в виду, что не во всех из них выбор показателя эффективности однозначно диктуется словесным описанием задачи, так что по этому вопросу возможны расхождения между читателем и автором.
1. План снабжения предприятий. Задача операции — обеспечить снабжение сырьем при минимальных расходах на перевозки. Показатель эффективности R — суммарные расходы на перевозки сырья за единицу времени, например, месяц (R =>
min).
2. Постройка участка магистрали. Требуется так спланировать строительство, чтобы закончить его как можно скорее. Естественным показателем эффективности было бы время завершения стройки, если бы оно не было связано со случайными факторами (отказы техники, задержки в выполнении отдельных работ). Поэтому в качестве показателя эффективности можно выбрать среднее ожидаемое время Т
окончания стройки (Т => min).
3. Продажа сезонных товаров. В качестве показателя эффективности можно взять среднюю ожидаемую прибыль П от реализации товаров за сезон (П => mах).
4. Снегозащита дорог. Речь идет о наиболее выгодном экономически плане снегозащиты, поэтому в качестве показателя эффективности можно выбрать средние за единицу времени (например, за год) расходы R на содержание и эксплуатацию дорог, включая расходы, связанные как с сооружением защитных устройств, так и с расчисткой дорог и задержками транспорта (R => min).
5. Противолодочный рейд. Так как рейд имеет вполне определенную цель А — уничтожение лодки, то в качестве показателя эффективности следует выбрать вероятность Р(A) того, что лодка будет уничтожена.
6. Выборочный контроль продукции. Естественный показатель эффективности, подсказанный формулировкой задачи, это средние ожидаемые расходы R на контроль за единицу времени, при условии, что система контроля обеспечивает заданный уровень качества, например, средний процент брака не выше заданного (R => min).
7. Медицинское обследование. В качестве показателя эффективности можно выбрать средний процент (долю) Q больных и носителей инфекции, которых удалось выявить (Q =>
шах).
8. Библиотечное обслуживание. В формулировке задачи сознательно допущена некоторая нечеткость:
неясно, что значит «наилучшее обслуживание абонентов» или «удовлетворение их запросов в максимальной мере». Если о качестве обслуживания судить по времени, которое запросивший книгу абонент ждет ее получения, то в качестве показателя эффективности можно взять среднее время Т
ожидания книги читателем, подавшим на нее заявку (Т => min). Можно подойти к вопросу и с несколько иных позиций, выбрав в качестве показателя эффективности среднее число М книг, выданных за единицу времени (М => mах).
Рассмотренные примеры специально подобраны настолько простыми, чтобы выбор показателя эффективности был сравнительно нетруден и прямо диктовался словесной формулировкой задачи, ее (почти всегда) однозначной целевой направленностью. Однако на практике это далеко не всегда бывает так. В этом читатель может убедиться, попытавшись, например, выбрать показатель эффективности работы городского транспорта. Что взять в качестве такого показателя? Среднюю скорость передвижения пассажиров по городу? Или среднее число перевезенных пассажиров? Или среднее количество километров, которое придется пройти пешком человеку, которого транспорт не может доставить к нужному месту? Тут есть над чем поразмыслить!
К сожалению, в большинстве задач, имеющих практическое значение, выбор показателя эффективности не прост и решается неоднозначно. Для сколько-нибудь сложной задачи типично положение, когда эффективность операции не может быть исчерпывающим образом охарактеризована одним единственным числом — на помощь ему приходится привлекать другие.
С такими «многокритериальными» задачами мы познакомимся в § 6.
§ 3. Математические модели операций
Для применения количественных методов исследования в любой области всегда требуется какая-то математическая модель. При построении модели реальное явление (в нашем случае — операция) неизбежно упрощается, схематизируется, и эта схема («макет» явления) описывается с помощью того или другого математического аппарата. Чем удачнее будет подобрана математическая модель, чем лучше она будет отражать характерные черты явления, тем успешнее будет исследование и полезнее — вытекающие из него рекомендации.
Общих способов построения математических моделей не существует. В каждом конкретном случае модель выбирается исходя из вида операции, ее целевой направленности, с учетом задачи исследования (какие параметры требуется определить и влияние каких факторов отразить). Необходимо также в каждом конкретном случае соразмерять точность и подробность модели: а) с той точностью, с которой нам нужно знать решение, и б) с той информацией, которой мы располагаем или можем приобрести. Если исходные данные, нужные для расчетов, известны неточно, то, очевидно, нет смысла входить в тонкости, строить очень подробную модель и тратить время (свое и машинное) на тонкую и точную оптимизацию решения. К сожалению, этим принципом часто пренебрегают и выбирают для описания явлений слишком подробные модели.
Математическая модель должна отражать важнейшие черты явления, все существенные факторы, от которых в основном зависит успех операции. Вместе с тем, модель должна быть по возможности простой, не «засоренной» массой мелких, второстепенных факторов: их учет усложняет математический анализ и делает труднообозримыми результаты исследования. Две опасности всегда подстерегают составителя модели: первая — увязнуть в подробностях («из-за деревьев не увидеть леса») и вторая—слишком огрубить явление («выплеснуть вместе с водой и ребенка»). Искусство строить математические модели есть именно искусство, и опыт в нем приобретается постепенно.
Поскольку математическая модель не вытекает с непреложностью из описания задачи, всегда полезно не верить слепо ни одной модели, а сличать результаты, полученные по разным моделям, устраивать как бы «спор моделей». При этом одну и ту же задачу решают не один раз, а несколько, пользуясь разной системой допущений, разным аппаратом, разными моделями. Если научные выводы от модели к модели меняются мало — это серьезный аргумент в пользу объективности исследования. Если они существенно расходятся, надо пересмотреть концепции, положенные в основу различных моделей, посмотреть, какая из них более адекватна действительности, в случае надобности — поставить контрольный эксперимент. Характерным для исследования операций является также повторное обращение к модели (после того, как первый тур расчетов уже проведен) для внесения в модель коррективов.
Создание математической модели — самая важная и ответственная часть исследования, требующая глубокого знания не столько математики, сколько существа моделируемых явлений. Как правило, «чистые» математики (без помощи специалистов в той области, к которой относится задача) с построением модели справляются плохо. В центре внимания у них оказывается математический аппарат с его тонкостями, а не реальная практическая задача.
Опыт показывает, что самые удачные модели создаются специалистами в данной области практики, получившими, в дополнение к основной, глубокую математическую подготовку, или же коллективами, объединяющими практиков-специалистов и математиков. Большую пользу приносят консультации, даваемые математиком, хорошо знающим исследование операций, практикам — инженерам, биологам, медикам и др., встречающимся в своей работе с необходимостью научного обоснования решений. От таких консультаций выигрывают не только практики, но и сам математик, знакомящийся с реальными задачами из самых разных областей. Для решения таких задач ему нередко приходится пополнять свое образование, а также развивать, обобщать и модифицировать известные ему методы.
Математическая подготовка специалиста, желающего самостоятельно (без посторонней помощи) заниматься исследованием операций в своей области практики, должна быть достаточно широка. Наряду с классическими разделами математического анализа (обычно проходимыми в вузе) в исследовании операций часто применяются современные, сравнительно новые разделы математики, такие, как линейное, нелинейное, динамическое программирование, теория игр и статистических решений, теория массового обслуживания и др. Некоторое понятие об этих разделах математики читатель может почерпнуть из нашей книги.
Специально надо подчеркнуть необходимость сведений по теории вероятностей — не столько обширных и глубоких, сколько неформальных, действенных, наличие привычки к оперированию со статистическими данными и вероятностными представлениями. Особые требования именно к этой области математических знаний объясняются тем, что большинство операций проводится в условиях неполной определенности, и их ход и исход зависят от случайных факторов. К сожалению, в широких кругах специалистов — инженеров, биологов, медиков, химиков — хорошее владение теорией вероятностей встречается редко. Ее положения и правила часто применяются формально, без подлинного понимания их смысла и духа. Нередко на теорию вероятностей смотрят как на некое подобие «волшебной палочки», позволяющее получить информацию «из ничего», из полного незнания. Это заблуждение: теория вероятностей позволяет только преобразовывать информацию, т. е. из сведений об одних явлениях, доступных наблюдению, делать выводы о других, недоступных. Наличие элементарных сведений по теории вероятностей предполагается у читателя этой книги.
Очень не хочется, чтобы перечисление разделов математики, применяемых в исследовании операций, запугало начинающего читателя и отбило у него охоту заниматься такими задачами. Во-первых, как говорится, не боги горшки обжигают, и любым аппаратом можно овладеть, если он действительно нужен. Во-вторых, не в каждой задаче применяются все перечисленные разделы; знакомиться можно не со всеми сразу, а с самыми необходимыми.
Какие знания по математике для каких задач нужны — можно опять-таки узнать из этой книги.
При построении математической модели может быть (в зависимости от вида операции, задач исследования и точности исходных данных) использован математический аппарат различной сложности. В самых простых случаях явление описывается простыми, алгебраическими уравнениями. В более сложных, когда требуется рассмотреть явление в динамике, применяется аппарат дифференциальных уравнений (обыкновенных или с частными производными). В наиболее сложных случаях, когда развитие операции, и ее исход зависят от большого числа сложно переплетающихся между собой случайных факторов, аналитические методы вообще отказываются служить, и применяется метод статистического моделирования (Монте-Карло), о котором будет идти речь в гл. 7. В первом, грубом приближении идею этого метода можно описать так: процесс развития операции, со всеми сопровождающими его случайностями, как бы «копируется», воспроизводится на машине (ЭВМ). В результате получается один экземпляр («реализация») случайного процесса развития операции со случайным ходом и исходом. Сама по себе одна такая реализация не дает оснований к выбору решения, но, получив множество таких реализации, мы обрабатываем его как обычный статистический материал (отсюда и термин «статистическое моделирование»), находим средние характеристики процесса и получаем представление о том, как в среднем влияют на них условия задачи и элементы решения.
В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений.
Статистические модели, по сравнению с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории — неограниченно большое) число факторов.
Но и у них — свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходится искать «на ощупь», путем догадок и проб.
Молодые специалисты, чей опыт в исследовании операций мал, имея в распоряжении вычислительные машины, часто без особой нужды начинают исследование с построения статистической модели, стараясь учесть в ней как можно больше факторов. Они забывают, что построить модель и произвести по ней расчеты — это полдела; важнее суметь проанализировать результаты и перевести их в ранг «рекомендаций».
Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей. Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить как бы «контур» основных закономерностей. Любые уточнения могут быть получены с помощью статистических моделей (подробнее см. главу 7).
В заключение скажем несколько слов о так называемом «имитационном» моделировании. Оно применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек (или группа людей), руководящий операцией, может, в зависимости от сложившейся обстановки, принимать те или другие решения, подобно тому, как шахматист, глядя на доску, выбирает свой очередной ход. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки в ответ на это решение и к каким последствиям оно приведет спустя некоторое время. Следующее «текущее решение» принимается уже с учетом реальной новой обстановки и т. д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучивается принимать правильные решения — если не оптимальные, то почти оптимальные. Такие процедуры, известные под названием «деловых игр», стали за последнее время очень популярными и, несомненно, полезны в деле подготовки управляющих кадров.
ГЛАВА 2
РАЗНОВИДНОСТИ ЗАДАЧ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ И ПОДХОДОВ К ИХ РЕШЕНИЮ
§ 4. Прямые и обратные задачи исследования операций. Детерминированные задачи
Задачи исследования операций делятся на две категории: а) прямые и б) обратные. Прямые задачи отвечают на вопрос: что будет, если в заданных условиях мы примем какое-то решение х

Для решения такой задачи строится математическая модель, позволяющая выразить один или несколько показателей эффективности через заданные условия и элементы решения.
Обратные задачи отвечают на вопрос: как выбрать решение х для того, чтобы показатель эффективности W обратился в максимум?
Естественно, прямые задачи проще обратных. Очевидно также, что для решения обратной задачи, прежде всего надо уметь решать прямую. Для некоторых типов операций прямая задача решается настолько просто, что ею специально не занимаются. Для других типов операций построение математических моделей и вычисление показателя (показателей) эффективности само по себе далеко не тривиально (так, например, обстоит дело с прямыми задачами теории массового обслуживания, с которыми мы встретимся в главе 6).
Остановимся несколько подробнее на обратных задачах. Если число возможных вариантов решения, образующих множество X. невелико, то можно попросту вычислить величину W для каждого из них, сравнить между собой полученные значения и непосредственно указать один или несколько оптимальных вариантов, для которых W
достигает максимума. Такой способ нахождения оптимального решения называется «простым перебором». Однако, когда число возможных вариантов решения, образующих множество X, велико, поиск среди них оптимального «вслепую», простым перебором, затруднителен, а зачастую практически невозможен. В этих случаях применяются методы «направленного перебора», обладающие той общей особенностью, что оптимальное решение находится рядом последовательных «попыток» или «приближений», из которых каждое последующее приближает нас к искомому оптимальному.
С некоторыми из таких методов мы познакомимся в главах 3 и 4.
Сейчас мы ограничимся постановкой задачи оптимизации решения (обратной задачи исследования операций) в самой общей форме.
Пусть имеется некоторая операция O, на успех которой мы можем в какой-то мере влиять, выбирая тем или другим способом решение х (напомним, что х — не число, а целая группа параметров). Пусть эффективность операции характеризуется одним показателем W => max.
Возьмем самый простой, так называемый «детерминированный» случай, когда все условия операции полностью известны заранее, т. е. не содержат неопределенности. Тогда все факторы, от которых зависит успех операции, делятся на две группы:
1) заданные, заранее известные факторы (условия выполнения операции), которые мы для краткости обозначим одной буквой а;
2) зависящие от нас элементы решения, образующие в своей совокупности решение х.
Заметим, что первая группа факторов содержит, в частности, и ограничения, налагаемые на решение, т. е. определяет область возможных решений X.
Показатель эффективности W зависит от обеих групп факторов. Это мы запишем в виде формулы:

При рассмотрении формулы (4.1) не надо забывать, что как х, так и ос в общем случае — не числа, а совокупности чисел (векторы), функции и т. д. В числе заданных условий к обычно присутствуют ограничения, налагаемые на элементы решения, имеющие вид равенств или неравенств.
Будем считать, что вид зависимости (4.1) нам известен, т. е. прямая задача решена. Тогда обратная задача формулируется следующим образом.
При
заданном комплексе условий

Этот максимум мы обозначим:
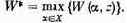
Формула (4.2) читается так: W* есть максимальное значение W(

К формулам такого типа надо привыкать. Они понадобятся в дальнейшем (см. гл. 4).
Итак, перед нами — типичная Математическая Задача нахождения максимума функции или функционала.
Эта задача принадлежит к классу так называемых «вариационных задач», хорошо разработанных в математике. Самые простые из таких задач («задачи на максимум и минимум») знакомы каждому инженеру. Чтобы найти максимум или минимум (короче, «экстремум») функции многих аргументов, надо продифференцировать ее по всем аргументам (в данном случае — элементам решения), приравнять производные нулю и решить полученную систему уравнений. Казалось бы, чего проще? А вот этот классический метод как раз в исследовании операций имеет весьма ограниченное применение. Во-первых, когда аргументов много, задача решения системы уравнений зачастую оказывается не проще, а сложнее, чем непосредственный поиск экстремума. Во-вторых, когда на элементы решения наложены ограничения, экстремум часто достигается не в точке, где производные равны нулю (такой точки может вообще не быть), а где-то на границе области X. Возникают все специфические трудности так называемой «многомерной вариационной задачи при ограничениях», иной раз непосильной по своей сложности даже для современных ЭВМ. Кроме того, в некоторых задачах функция W вообще не имеет производных (например, задана только для целочисленных значений аргументов). Все это делает задачу поиска экстремума далеко не такой простои, как она кажется с первого взгляда.
Метод поиска экстремума и связанного с ним оптимального решения х* должен всегда выбираться исходя из особенностей функции W и вида ограничений, накладываемых на решение. Например, если функция W линейно зависит от элементов решения x1, x2, ..., а ограничения, налагаемые на x1, x2, ..., имеют вид линейных равенств или неравенств, возникает ставшая классической задача линейного программирования, которая решается сравнительно простыми, а главное, стандартными методами (см. главу 3). Если функция W выпукла, применяются специальные методы выпуклого программирования с их разновидностью:
«квадратичным программированием» (см. [8]). Для оптимизации управления многоэтапными операциями применяется метод динамического программирования (см.
главу 4). Наконец, существует целый набор численных методов отыскания экстремумов, специально приспособленных для реализации на ЭВМ; некоторые из них включают элемент «случайного поиска», который для многомерных задач нередко оказывается эффективнее упорядоченного перебора.
Таким образом, задача нахождения оптимального решения в простейшем, детерминированном случае есть чисто математическая задача, принадлежащая к классу вариационных (при отсутствии или наличии ограничений), которая может представить вычислительные, но не принципиальные трудности. Не так обстоит дело в случае, когда задача содержит элемент неопределенности.
§ 5. Проблема выбора решения в условиях неопределенности
В предыдущем параграфе мы рассмотрели обратную задачу исследования операций в детерминированном случае, когда показатель эффективности W зависит только от двух групп факторов: заданных, заранее известных а и элементов решения х. Реальные задачи исследования операций чаще всего содержат помимо этих двух групп еще одну — неизвестные факторы, которые в совокупности мы обозначим одной буквой ?. Итак, показатель эффективности W
зависит от всех трех групп факторов:
W=W(a, х, ?). (5.1)
Так как величина W зависит от неизвестных факторов ? то даже при заданных

При заданных условиях


Это уже другая, не чисто математическая задача (недаром в ее формулировке сделана оговорка «по возможности»).
Наличие неопределенных факторов ? переводит задачу в новое качество: она превращается в задачу о выборе решения в условиях неопределенности.
Порассуждаем немного о возникшей задаче. Прежде всего, будем честны: неопределенность есть неопределенность, и ничего хорошего в ней нет. Если условия операции неизвестны, мы не можем так же успешно оптимизировать решение, как мы это сделали бы, если бы располагали большей информацией. Поэтому любое решение, принятое в условиях неопределенности, хуже решения, принятого в заранее известных условиях. Что делать? Плохое или хорошее — решение все равно должно быть принято. Наше дело — придать этому решению в возможно большей мере черты разумности. Недаром Т. Л. Саати, один из видных зарубежных специалистов по исследованию операций, определяя свой предмет, говорит не без иронии: «Исследование операций представляет собой искусство давать плохие ответы на практические вопросы, на которые даются еще худшие ответы другими методами».
Задача принятия решения в условиях неопределенности на каждом шагу встречается нам в жизни. Например, мы собрались путешествовать, и укладываем в чемодан вещи. Размеры и вес чемодана, а также имеющийся у нас набор вещей заданы (условия

Теперь возьмем более серьезную задачу. Планируется ассортимент товаров для распродажи на ярмарке. Желательно было бы максимизировать прибыль. Однако заранее неизвестно ни количество покупателей, которые придут на ярмарку, ни потребности каждого из них. Как быть? Неопределенность налицо, а принимать решение нужно!
Другой пример: проектируется система сооружений, оберегающих район от паводков. Ни моменты их наступления, ни размеры заранее неизвестны. А проектировать все-таки нужно, и никакая неопределенность не избавит нас от этой обязанности...
Наконец, еще более сложная задача: разрабатывается план развития вооружения на несколько лет вперед. Неизвестны ни конкретный противник, ни вооружение, которым он будет располагать. А решение принимать надо!
Для того чтобы такие решения принимать не наобум, по вдохновению, а трезво, с открытыми глазами, современная наука располагает рядом приемов. Каким из них воспользоваться — зависит от того, какова природа неизвестных факторов ?, откуда они возникают и кем контролируются. Другими словами, с какого вида неопределенностью мы в данной задаче сталкиваемся?
У читателя может возникнуть вопрос: неужели можно классифицировать неопределенности по «родам» и «сортам»? Оказывается, можно.
Прежде всего, рассмотрим наиболее благоприятный для исследования, так сказать, «доброкачественный» вид неопределенности. Это случай, когда неизвестные факторы ? представляют собой обычные объекты изучения теории вероятностей — случайные величины (или случайные функции), статистические характеристики которых нам известны или в принципе могут быть получены к нужному сроку. Такие задачи исследования операций мы будем называть стохастическими задачами, а присущую им неопределенность — стохастической неопределенностью.
Приведем пример стохастической задачи исследования операций. Пусть организуется или реорганизуется работа столовой с целью повысить ее пропускную способность. Нам в точности неизвестно, какое количество посетителей придет в нее за рабочий день, когда именно они будут появляться, какие блюда заказывать и сколько времени будет продолжаться обслуживание каждого из них.
Однако характеристики этих случайных величин, если сейчас еще не находятся в нашем распоряжении, могут быть получены статистическим путем.
Другой пример: организуется система профилактического и аварийного ремонта технических устройств с целью уменьшить простои техники за счет неисправностей и ремонтов. Отказы техники, длительности ремонтов и профилактик носят случайный характер. Характеристики всех случайных факторов, входящих в задачу, могут быть получены, если собрать соответствующую статистику.
Рассмотрим более подробно этот «доброкачественный» вид неопределенности. Пусть неизвестные факторы ? представляют собой случайные величины с какими-то, в принципе известными, вероятностными характеристиками — законами распределения, математическими ожиданиями, дисперсиями и т. п. Тогда показатель эффективности W, зависящий от этих факторов, тоже будет величиной случайной. Максимизировать случайную величину невозможно: при любом решении х она остается случайной, неконтролируемой. Как же быть?
Первое, что приходит в голову: а нельзя ли заменить случайные факторы ? их средними значениями (математическими ожиданиями)? Тогда задача становится детерминированной и может быть решена обычными методами.
Что и говорить — прием соблазнительный и в некоторых случаях даже оправданный. Ведь на практике, решая большинство задач физики, механики, техники, мы сплошь и рядом им пользуемся, пренебрегая случайностью ряда параметров (теплоемкость, индуктивность, коэффициент трения) и заменяя их средними значениями. Весь вопрос в том, насколько случайны эти параметры: если они мало отклоняются от своих математических ожиданий, так поступать можно и нужно. Так же обстоит дело и в исследовании операций: есть задачи, в которых случайностью можно пренебречь. Например, если мы составляем план снабжения группы предприятий сырьем (см. пример 1 § 1), можно в первом приближении пренебречь, скажем, случайностью фактической производительности источников сырья (если, разумеется, его производство хорошо налажено).
Тот же прием — пренебречь случайностью и заменить все входящие в задачу случайные величины их математическими ожиданиями — будет уже опрометчивым, если влияние случайности па интересующий нас исход операции существенно. Возьмем самый грубый пример: пусть мы ведем обстрел какой-то цели, стремясь, во что бы то пи стало попасть в нее. Производится несколько выстрелов. Давайте, заменим все случайные координаты точек попадания их математическим ожиданием — центром цели. Получится, что любой выстрел с гарантией попадет в цель, что заведомо неверно. Другой, менее очевидный, пример: планируется работа ремонтной мастерской, обслуживающей автобазу. Пренебрежем случайностью момента появления неисправности (т. е. заменим случайное время безотказной работы машины его математическим ожиданием) и случайностью времени выполнения ремонта. И что же окажется? Мастерская, работа которой спланирована без учета случайности, попросту не будет справляться со своей задачей (в этом мы убедимся в главе 6). Встречаются (и очень часто) операции, в которые случайность входит по существу, и свести задачу к детерминированной не удается.
Итак, рассмотрим такую операцию O, где факторы ? «существенно случайны» и заметно влияют на показатель эффективности W, который тоже «существенно случаен».
Возникает мысль: надо взять в качестве показателя эффективности среднее значение (математическое ожидание) этой случайной величины W= M[W] и выбрать
такое решение х, при котором этот усредненный по условиям показатель обращается в максимум:
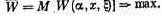
Заметим, что именно так мы поступали в § 2, выбирая в качестве показателя эффективности в задачах, содержащих неопределенность, не просто «доход», а «средний доход», не просто «время», а «среднее время». В большинстве случаев такой подход (мы его назовем «оптимизацией в среднем») вполне оправдан. В самом деле, если мы выберем решение так, чтобы среднее значение показателя эффективности обращалось в максимум, то, безусловно, поступим правильнее, чем, если бы выбирали решение наобум.
А как же с элементом неопределенности? Конечно, в какой- то мере он сохраняется. Эффективность каждой отдельной операции, проводимой при конкретных значениях случайных факторов ?, может сильно отличаться от ожидаемой как в большую, так, к сожалению, и в меньшую сторону. Нас может утешить то, что, оптимизируя операцию «в среднем», мы, в конечном счете, после многих ее повторений выиграем больше, чем, если бы совсем не пользовались расчетом.
Такая «оптимизация в среднем» очень часто применяется на практике в стохастических задачах исследования операций, и пользуются ею обычно не задумываясь над ее правомочностью. А задуматься надо! Чтобы этот прием был законным, нужно, чтобы операция обладала свойством повторяемости, и «недостача» показателя эффективности в одном случае компенсировалась его «избытком» в другом. Например, если мы предпринимаем длинный ряд однородных операций с целью получить максимальный доход, то доходы от отдельных операций суммируются, «минус» в одном случае покрывается «плюсом» в другом, и все в порядке.
Всегда ли это будет так? Нет, не всегда! Чтобы убедиться в этом, рассмотрим пример. Организуется автоматизированная система управления (АСУ) для службы неотложной медицинской помощи большого города. Вызовы, возникающие в разных районах города в случайные моменты, поступают на центральный пункт управления, откуда они передаются на тот или другой пункт неотложной помощи с приданными ему машинами. Требуется разработать такое правило (алгоритм) диспетчерской работы АСУ, при котором служба в целом будет функционировать наиболее эффективно. Для этого, прежде всего, надо выбрать показатель эффективности W.
Разумеется, желательно, чтобы время Т ожидания врача было минимально. Но это время — величина случайная. Если применить «оптимизацию в среднем», то надо выбрать тот алгоритм, при котором среднее время ожидания минимально. Не так ли?
Оказывается, не совсем так! Беда в том, что времена ожидания врача отдельными больными не суммируются: слишком долгое ожидание одного из них не компенсируется почти мгновенным обслуживанием другого.
Выбирая в качестве показателя эффективности среднее время ожидания Т, мы рискуем дать предпочтение тому алгоритму, при котором среднее-то время ожидания мало, но отдельные больные могут ожидать врача очень долго! Чтобы избежать таких неприятностей, можно дополнить показатель эффективности добавочным требованием, чтобы фактическое время Т
ожидания врача было не больше какого-то предельного значения t0. Поскольку Т — величина случайная, нельзя просто потребовать, чтобы выполнялось условие Т





Р (Т



Введение такого ограничения означает, что из области возможных решений Х исключаются решения, ему не удовлетворяющие. Ограничения типа (5.3) называются стохастическими ограничениями; наличие таких ограничений сильно усложняет задачу оптимизации.
Особенно осторожным надо быть с «оптимизацией в среднем», когда речь идет не о повторяемой, массовой операции, а о единичной, «уникальной». Все зависит от того, к каким последствиям может привести неудача данной операции, т. е. слишком малое значение показателя эффективности W; иногда оно может означать попросту катастрофу. Что толку в том, что операция в среднем приносит большой выигрыш, если в данном, единичном случае она может нас дотла разорить? От таких катастрофических результатов можно опять-таки спасаться введением стохастических ограничений. При достаточно большом значении уровня доверия

Итак, мы вкратце рассмотрели случай «доброкачественной» (стохастической) неопределенности и в общих чертах осветили вопрос об оптимизации решения в таких задачах.
Но это, как говорится, цветочки, ягодки будут впереди! Стохастическая неопределенность — это почти определенность, если только известны вероятностные характеристики входящих в задачу случайных факторов. Гораздо хуже обстоит дело, когда неизвестные факторы ? не могут быть изучены и описаны статистическими методами. Это бывает в двух случаях: либо а) распределение вероятностей для параметров 1 в принципе существует, но к моменту принятия решения не может быть получено, либо б) распределение вероятностей для параметров ? вообще не существует.
Пример ситуации типа а): проектируется информационно-вычислительная система (ИВС), предназначенная для обслуживания каких-то случайных потоков требований (запросов). Вероятностные характеристики этих потоков требований в принципе могли бы быть получены из статистики, если бы данная ИВС (или аналогичная ей) уже существовала и функционировала достаточно долгое время. Но к моменту создания проекта такой информации нет, а решение принимать надо! Как быть?
Разумеется, можно заранее (из умозрительных соображений) задаться какими-то характеристиками случайных факторов ? оптимизировать решение х
на этой основе (просто «в среднем» или при стохастических ограничениях) и остановиться па нем. Это будет, безусловно, лучше, чем выбрать решение наобум, но не намного лучше. Гораздо разумнее будет применить следующий прием: оставить некоторые элементы решения х свободными, изменяемыми. Затем выбрать для начала какой-то вариант решения, зная заведомо, что он не самый лучший, и пустить систему в ход, а потом, по мере накопления опыта, целенаправленно изменять свободные параметры решения, добиваясь того, чтобы эффективность не уменьшалась, а увеличивалась. Такие совершенствующиеся в процессе применения алгоритмы управления называются адаптивными. Преимущество адаптивных алгоритмов в том, что они не только избавляют пас от предварительного сбора статистики, по н перестраиваются в ответ па изменение обстановки. По мере накопления опыта такой алгоритм постепенно улучшается, подобно тому, как живой человек «учится па ошибках».
Теперь обратимся к самому трудному и неприятному случаю б), когда у неопределенных факторов ? вообще не существует вероятностных характеристик;
другими словами, когда их нельзя считать «случайными» в обычном смысле слова.
— Как? — может быть, спросит читатель.— Разве не всякая неопределенность есть случайность?
— Нет,— ответим мы,— лучше не путать эти понятия.
Поясняем: под термином «случайное явление» в теории вероятностей принято понимать явление, относящееся к классу повторяемых и, главное, обладающее свойством статистической устойчивости. При повторении однородных опытов, исход которых случаен, их средние характеристики проявляют тенденцию к устойчивости, стабилизируются. Частоты событий приближаются к их вероятностям, средние арифметические — к математическим ожиданиям. Если много раз бросать монету, частота появления герба постепенно стабилизируется, перестает быть случайной; если много раз взвешивать па аналитических весах одно и то же тело, средний результат перестает колебаться, выравнивается. Это пример доброкачественной, стохастической неопределенности.
Однако бывает неопределенность и нестохастнческого вида, которую мы условно назовем «дурной неопределенностью». Несмотря на то, что факторы t заранее неизвестны, не имеет смысла говорить об их «законах распределения» или других вероятностных характеристиках.
Пример: допустим, планируется некая торгово-промышленная операция, успех которой зависит от того, юбки какой длины ? будут носить женщины через два года. Распределение вероятностей для величины ? в принципе не может быть получено ни из каких статистических данных. Даже если рассмотреть великое множество опытов (годов), начиная с тех отдаленных времен, когда женщины впервые надели юбки, и в каждом из них зарегистрировать величину ?, это вряд ли поможет нам в нашем прогнозе. Вероятностное распределение величины ? попросту не существует, так как не существует массива однородных опытов, где она обладала бы должной устойчивостью. Налицо случай «дурной неопределенности».
Как же все-таки быть в таких случаях? Отказаться вообще от применения математических методов и выбрать решение «волевым» образом? Нет, этого делать не стоит. Некоторую пользу предварительные расчеты могут принести даже в. таких скверных условиях.
Давайте поразмышляем на эту тему. Пусть выбирается решение х
в какой-то операции O,
условия которой содержат «дурную неопределенность» — параметры ?, относительно которых никаких сведений мы не имеем, а можем делать лишь предположения. Попробуем все же решить задачу.
Первое, что приходит в голову: а ну-ка, зададимся какими-то, более или менее правдоподобными, значениями параметров ?. Тогда задача перейдет в категорию детерминированных и может быть решена обычными методами (детерминированный случай, со всеми его трудностями, представляется нам теперь чуть ли не «курортом»!).
Нет, радоваться рано. Допустим, что, затратив много усилий и времени (своего и машинного), мы это сделали. Ну и что? Будет ли найденное решение хорошим для других условий ?. Как правило, нет. Поэтому ценность его — сугубо ограниченная. В данном случае разумно будет выбрать не решение х,
оптимальное для каких-то условий ?, а некое компромиссное решение, которое, не будучи оптимальным, может быть, ни для каких условий, будет все же приемлемым в целом их диапазоне.
В настоящее время полноценной научной теории компромисса не существует, хотя некоторые попытки в этом направлении в теории игр и статистических решений делаются (см. главу 8). Обычно окончательный выбор компромиссного решения осуществляется человеком. Опираясь па предварительные расчеты, в ходе которых решается большое число прямых задач исследования операций для разных условий ? и разных вариантов решения х, он может оценить сильные и слабые стороны каждого варианта и на этой основе сделать выбор. Для этого необязательно (хотя иногда и любопытно) знать точный «условный» оптимум для каждой совокупности условий ?. Математические вариационные методы в данном случае отступают на задний план.
Подчеркнем еще одну полезную функцию предварительных математических расчетов в задачах с «дурной неопределенностью»: они помогают заранее отбросить те решения х

иногда — свести его к небольшому числу вариантов, которые легко могут быть просмотрены и оценены человеком в поисках удачного компромисса.
При рассмотрении задач исследования операций с «дурной неопределенностью» всегда полезно сталкивать в споре разные подходы, разные точки зрения. Среди последних надо отметить одну, часто применяемую в силу своей математической определенности, которую можно назвать «позицией крайнего пессимизма». Она сводится к тому, что, принимая решение в условиях «дурной неопределенности», надо всегда рассчитывать на худшее и принимать то решение, которое дает максимальный эффект в наихудших условиях. Если в этих условиях мы получаем выигрыш W =

Вряд ли такому военачальнику будет сопутствовать удача! Напротив, в любой конкретной ситуации нужно стараться угадать, в чем слаб и «глуп» противник, и стараться «обвести его вокруг пальца». Тем менее уместен крайне пессимистический подход в ситуациях, где стороне, принимающей решение, не противостоят никакие враждебные силы. Расчеты, основанные на точке зрения «крайнего пессимизма», всегда должны корректироваться разумной долей оптимизма. Вряд ли стоит становиться и на противоположную точку зрения — крайнего пли «залихватского» оптимизма, но известная доля риска при принятии решения все же должна присутствовать. Нельзя также забывать о том, что любое решение, принятое в условиях «дурной неопределенности»,— неизбежно плохое решение, и вряд ли стоит обосновывать его с помощью тонких и кропотливых расчетов. Скорее следует подумать о том, откуда можно было бы взять недостающую информацию. Здесь все способы хороши — лишь бы прояснить положение.
Упомянем в этой связи об одном довольно оригинальном методе, не пользующемся любовью в среде чистых математиков, но тем не менее полезном, а иногда — единственно возможном. Речь идет о так называемом методе экспертных оценок. Он часто применяется в задачах, связанных с прогнозированием в условиях дурной неопределенности (например, в футурологии). Грубо говоря, идея метода сводится к следующему: собирается коллектив сведущих, компетентных в данной области людей, и каждому из них предлагается ответить на какой-то вопрос (например, назвать срок, когда будет совершено то или другое открытие, пли оценить вероятность того или другого события). Затем полученные ответы обрабатываются наподобие статистического материала. Результаты обработки, разумеется, сохраняют субъективный характер, но в гораздо меньшей степени, чем, если бы мнение высказывал один эксперт («ум хорошо, а два — лучше»). Подобного рода экспертные оценки для неизвестных условий могут быть применены и при решении задач исследования операций с дурной неопределенностью. Каждый из экспертов па глаз оценивает степень правдоподобия различных вариантов условий 1, приписывая им какие-то субъективные вероятности.
Несмотря на субъективный характер оценок каждого эксперта, усредняя оценки целого коллектива, можно получить нечто более объективное и полезное (кстати, оценки разных экспертов расходятся не так сильно, как можно было бы ожидать). Таким образом, задача с дурной неопределенностью как бы сводится к обычной стохастической задаче. Разумеется, к полученным отсюда выводам не надо относиться слишком доверчиво, но наряду с другими результатами, вытекающими из других точек зрения, но все же могут помочь при выборе решения.
Наконец, сделаем одно общее замечание. При обосновании решения в условиях неопределенности, что бы мы ни делали, элемент неопределенности, «гадательности» сохраняется. Поэтому нельзя предъявлять к точности решений слишком высокие требования. Вместо того чтобы указать одно-единственное, в точности «оптимальное» (с какой-то точки зрения) решение, лучше выделить целую область «приемлемых» решений, которые оказываются несущественно хуже других, какой бы точкой зрения мы ни пользовались. В пределах этой области и должны производить свой окончательный выбор ответственные за это люди. Исследователь, предлагая им рекомендации по выбору решения, всегда должен одновременно указывать точки зрения, из которых вытекают те или другие рекомендации.
§ 6. Многокритериальные задачи исследования операций. «Системный подход»
Несмотря на ряд существенных трудностей, связанных с неопределенностью, мы до сих пор рассматривали только самые простые случаи, когда ясен критерий, по которому производится оценка эффективности, и требуется обратить в максимум (минимум) один-единственный показатель W. К сожалению, на практике такие задачи, где критерий оценки однозначно диктуется целевой направленностью операции, встречаются не так уж часто — преимущественно при рассмотрении небольших по масштабу и скромных по значению мероприятий. А когда идет речь о крупномасштабных, сложных операциях, затрагивающих разнообразные интересы их организаторов и общества в целом, то их эффективность, как правило, не может быть полностью охарактеризована с помощью одного-• единственного показателя эффективности W. На помощь ему приходится привлекать другие, дополнительные.
Такие задачи исследования операций называются многокритериальными.
Рассмотрим пример такой задачи. Организуется оборона важного объекта от воздушных налетов. В нашем распоряжении — какие-то средства противовоздушной обороны, которые надо разумным образом разместить вокруг объекта, организовать их взаимодействие, распределить между ними цели, назначить боезапас и т. д. Допустим, что каждый из самолетов противника, участвующих в налете, является потенциальным носителем мощного поражающего средства, которое, будучи применено по объекту, гарантирует его уничтожение. Тогда главная задача операции — не допустить к объекту ни одного самолета, а естественный показатель эффективности — вероятность W того, что ни один самолет не прорвется к объекту. Но единственный ли это важный для нас показатель? Безусловно, нет. При одной и той же вероятности W мы предпочтем все-таки решение, при котором будет погибать в среднем побольше самолетов противника. Отсюда второй показатель эффективности М — среднее число пораженных целей, который нам тоже хотелось бы максимизировать. Кроме того, нам далеко не все равно, каковы будут наши собственные боевые потери П — еще один критерий, который хотелось бы минимизировать. Желательно было бы, кроме того, сделать поменьше средний расход боеприпасов R, и т. д.
Другой пример — на этот раз из совершенно мирной области. Организуется (или реорганизуется) работа промышленного предприятия. Под углом зрения какого критерия надо выбирать решение? С одной стороны, нам хотелось бы обратить в максимум валовый объем продукции V. Желательно также было бы получить максимальный чистый доход D. Что касается себестоимости S, то ее хотелось бы обратить в минимум, а производительность труда П — в максимум. При обдумывании задачи может возникнуть еще ряд дополнительных критериев.
Такая множественность показателей эффективности, из которых одни желательно обратить в максимум, а другие — в минимум, характерна для любой сколько-нибудь сложной задачи исследования операций.
Предлагаем читателю в виде упражнения попытаться сформулировать ряд критериев, по которым будет оцениваться работа автобусного парка. Подумайте о том, какой из них, с вашей точки зрения, является главным (теснее всего связанным с целевой направленностью операции), а остальные (дополнительные) расположите в порядке убывающей важности. На этом примере можно убедиться в том, что а) ни один из показателей не может быть выбран в качестве единственного и б) формулировка системы показателей — не такая уж простая задача... И сами показатели, и их упорядоченность по важности зависят от того, с точки зрения, чьих интересов оптимизируется решение.
Итак, типичной для крупномасштабной задачи исследования операций является многокритериальность — наличие ряда количественных показателей W1, W2,…, одни из которых желательно обратить в максимум, другие — в минимум («чтобы и волки были сыты, и овцы целы»).
Спрашивается, можно ли найти решение, одновременно удовлетворяющее всем этим требованиям? Со всей откровенностью ответим: нет. Решение, обращающее в максимум один какой-то показатель, как правило, не обращает ни в максимум, ни в минимум другие. Поэтому часто применяемая формулировка: «достигнуть максимального эффекта при минимальных затратах» представляет собой не более чем фразу и при научном анализе должна быть отброшена.
Как же быть в случае, если все же приходится оценивать эффективность операции по нескольким показателям?
Люди, малоискушенные в исследовании операции, обычно торопятся свести многокритериальную задачу к однокритериальной: составляют какую-то функцию от всех показателей и рассматривают ее как один, «обобщенный» показатель, по которому и оптимизируется решение. Часто такой обобщенный показатель имеет вид дроби, в числителе которой стоят все величины, увеличение которых желательно, а в знаменателе — то, увеличение которых нежелательно. Например, продуктивность и доход — в числителе, время выполнения и расходы — в знаменателе и т. д.
Такой способ объединения нескольких показателей в один не может быть рекомендован, и вот почему: он основан на неявном допущении, что недостаток в одном показателе всегда может быть скомпенсирован за счет другого; например, малая продуктивность — за счет низкой стоимости и т.
д. Это, как правило, несправедливо.
Вспомним «критерий для оценки человека», полушутя-полусерьезно предложенный когда- то Львом Толстым. Он имеет вид дроби, в числителе которой стоят действительные достоинства человека, а в знаменателе — его мнение о себе. С первого взгляда такой подход может показаться логичным. Но представим себе человека, почти совсем не имеющего достоинств, по совсем не обладающего самомнением. По критерию Л. Н. Толстого такой человек должен иметь бесконечно большую ценность, с чем уж никак согласиться нельзя.
К подобным парадоксальным выводам может привести (и нередко приводит) пользование показателем в виде дроби, где, как говорят, все, что «за здравие»,— в числителе, все, что «за упокой»,— в знаменателе.
Нередко применяется и другой, чуть более замысловатый, способ составления «обобщенного показателя эффективности»— он представляет собой «взвешенную сумму» частных показателей, в которую каждый из них Wi входит с каким-то «весом» ai, отражающим его важность:
W =a1 W1
+a2 W2 +... (6.1)
(для тех показателей, которые желательно увеличить, веса берутся положительными, уменьшить — отрицательными).
При произвольном назначении весов a1, а2, ... этот способ ничем не лучше предыдущего (разве тем, что обобщенный критерий не обращается в бесконечность). Его сторонники ссылаются на то, что и человек, принимая компромиссное решение, тоже мысленно взвешивает все «за» и «против», приписывая больший вес более важным для него факторам. Это, может быть, и так, но, по-видимому, «весовые коэффициенты», с которыми входят в расчет разные показатели, не постоянны, а меняются в зависимости от ситуации.
Поясним это элементарным примером. Человек выходит из дому, чтобы ехать на работу, боится опоздать и размышляет: каким транспортом воспользоваться? Трамвай ходит часто, но идет долго; автобус — быстрее, но с большими интервалами. Можно, конечно, взять такси, но это обойдется дорого. Есть еще такое решение: часть пути проехать на метро, а затем взять такси.
Но на стоянке может не быть машин, а, добираясь до работы со станции метро пешком, он рискует опоздать больше, чем, если бы ехал автобусом. Как ему поступить?
Перед нами типичная (намеренно упрощенная) задача исследования операций с двумя критериями (показателями). Первый — среднее ожидаемое время опоздания Т,
которое хотелось бы сделать минимальным. Второй — ожидаемая стоимость проезда S; ее тоже желательно сделать минимальной. Но эти два требования, как мы знаем, несовместимы, поэтому человек должен принять компромиссное, приемлемое по обоим критериям, решение. Возможно, он при этом подсознательно взвешивает все «за» и «против», пользуясь чем-то вроде обобщенного показателя:
W = a1 T + a2 S => min. (6.2)
Но беда в том, что весовые коэффициенты а1, а2 никак нельзя считать постоянными. Они зависят как от самих величин Т
и S, так и от обстановки. Например, если человек недавно уже получил выговор за опоздание, коэффициент при Т у него, вероятно, увеличится, а на другой день после получки, вероятно, уменьшится коэффициент при S.
Если же назначать (как это обычно и делается) веса а1, а2
произвольно, то, по существу, столь же произвольным будет и вытекающее из них «оптимальное» решение.
Здесь мы встречаемся с очень типичным для подобных ситуаций приемом — «переносом произвола из одной инстанции в другую». Простой выбор компромиссного решения на основе мысленного сопоставления всех «за» и «против» каждого решения кажется слишком произвольным, недостаточно «научным». А вот маневрирование с формулой, включающей (пусть столь же произвольно назначенные) коэффициенты а1, а2, ...,—совсем другое дело. Это уже «наука»! По существу же никакой науки тут нет, и нечего обманывать самих себя.
«Гони природу в дверь — она влетит в окно». Нечего надеяться полностью, избавиться от субъективности в задачах, связанных с выбором решений. Даже в простейших, однокритериальных задачах она неизбежно присутствует, проявляясь хотя бы в выборе показателя эффективности и математической модели явления.
Тем более неизбежна субъективность ( грубо говоря, произвол) при выборе решения в многокритериальной задаче. Правда, бывают редкие случаи, когда достаточно ознакомиться со значениями всех показателей для каждого варианта, чтобы сразу стало ясно, какой из них выбрать. Представим себе, например, что какой-то вариант решения х имеет преимущество над другими по всем показателям; ясно, что именно его следует предпочесть. Но гораздо чаще встречаются случаи, когда с первого взгляда ситуация неясна: один из показателей тянет в одну сторону, другой — в другую. При этом всегда полезно провести дополнительные расчеты, пользуясь, может быть, даже формулами типа (6.1), но, не доверяя им слепо, а сохраняя к ним критическое отношение.
Выходит, что математический аппарат не может нам ничем помочь при решении многокритериальных задач? Отнюдь нет, он может помочь, и очень существенно. Прежде всего, он позволяет решать прямые задачи исследования операций, т. е. для любого решения х находить значения показателей эффективности W1, W2, ..., сколько бы их ни было (кстати, для прямых задач многокритериальность — не помеха). И во-вторых, что особенно важно, он помогает «выбраковать» из множества возможных решений Х заведомо неудачные, уступающие другим по всем критериям.
Покажем, как это, в принципе, делается. Пусть имеется многокритериальная задача исследования операций с k критериями. W1, W2, …, Wk. Для простоты предположим, что все эти величины желательно максимизировать (как переходить от «минимума» к «максимуму», мы уже знаем). Пусть в составе множества возможных решений есть два решения х1 и х2 такие, что все критерии W1, W2, .., Wk для первого решения больше или равны соответствующим критериям для второго решения, причем хотя бы один из них действительно больше. Очевидно, тогда в составе множества Х нет смысла сохранять решение х2, оно вытесняется (или, как говорят, «доминируется») решением х1.
Ладно, выбросим, решение x2 как неконкурентоспособное и перейдем к сравнению других по всем критериям.
В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество Х обычно сильно уменьшается: в нем сохраняются только так называемые эффективные (иначе «паретовские») решения, характерные тем, что ни для одного из них не существует доминирующего решения.
Проиллюстрируем прием выделения паретовских решений на примере задачи с двумя критериями: W1 и W2 (оба требуется максимизировать). Множество Х состоит из конечного числа п возможных решений х1, x2, ..., xn. Каждому решению соответствуют определенные значения показателей W1, W2; будем изображать решение точкой на плоскости с координатами W1, W2 и занумеруем точки соответственно номеру решения (рис. 6.1).
 |
лежащие на правой верхней границе области возможных решений (см. жирные точки, соединенные пунктиром, на рис. 6.1). Для всякого другого решения существует хотя бы одно доминирующее, для которого либо W1, либо W2, либо оба больше, чем для данного. И только для решений, лежащих на правой верхней границе, доминирующих не существует.
Когда из множества возможных решений выделены эффективные, «переговоры» могут вестись уже в пределах этого - «эффективного» множества. На рис. 6.1 его образуют четыре решения: x2, x5, х10
и x11; из них x11 — наилучшее по критерию W1, х2 — по критерию W2. Дело лица, принимающего решение, выбрать тот вариант, который для него предпочтителен и «приемлем» по обоим критериям.
Аналогично строится множество эффективных решений и в случае, когда показателей не два, а больше (при числе их, большем трех, геометрическая интерпретация теряет наглядность, но суть дела сохраняется). Множество эффективных решений легче обозримо, чем множество X. Что касается окончательного выбора решения, то он по-прежнему остается прерогативой человека. Только человек, с его непревзойденным умением решать неформальные задачи, принимать так называемые «компромиссные решения» (не строго-оптимальные, но приемлемые по ряду критериев) может взять на себя ответственность за окончательный выбор.
Однако сама процедура выбора решения, будучи повторена неоднократно, может послужить основой для выработки некоторых формальных правил, применяемых уже без участия человека. Речь идет о так называемых «эвристических» методах выбора решений. Предположим, что опытный человек (или, еще лучше, группа опытных людей) многократно выбирает компромиссное решение в многокритериальной задаче исследования операций, решаемой при разных условиях а. Набирая статистику по результатам выбора, можно, например, разумным образом подобрать значения «весов» a1, a2, … в формуле. (6.1), в общем случае зависящие от условий » и самих показателей W1, W2, ..., и воспользоваться таким обобщенным критерием для выбора решения, на этот раз уже автоматического, без участия человека. На это иногда приходится идти в случаях, когда времени на обдумывание компромиссного решения нет (например, в условиях боевых действий), или же в случае, когда выбор решения передается автоматизированной системе управления (АСУ).
В некоторых случаях очень полезной оказывается процедура выбора решения в так называемом «диалоговом режиме», когда машина, произведя расчеты, выдает лицу (лицам), управляющему операцией, значения показателей W1, W2, ..., а это лицо, критически оценив ситуацию, вносит изменения в весовые коэффициенты (или иные параметры управляющего алгоритма).
Существует один, часто применяемый способ свести многокритериальную задачу к однокритериальной — это выделить один (главный) показатель W1 и стремиться его обратить в максимум, а на все остальные W2, W3, ... наложить только некоторые ограничения, потребовав, чтобы они были не меньше каких-то заданных w2, w3, … Например, при оптимизации плана работы предприятия можно потребовать, чтобы прибыль была максимальна, план по ассортименту — выполнен или перевыполнен, а себестоимость продукции — не выше заданной. При таком подходе все показатели, кроме одного — главного, переводятся в разряд заданных условий ос. Известный произвол в назначении границ w2, w3, ..., разумеется, при этом остается; поправки в эти границы тоже могут быть введены в «диалоговом режиме».
Существует еще один путь построения компромиссного решения, который можно назвать «методом последовательных уступок». Предположим, что показатели W1, W2,... расположены в порядке убывающей важности. Сначала ищется решение, обращающее в максимум первый (важнейший) показатель W1 = W1*. Затем назначается, исходя из практических соображений, с учетом малой точности, с которой нам известны входные данные, некоторая «уступка»



Так или иначе, при любом способе ее постановки, задача обоснования решения по нескольким показателям остается не до конца формализованной, и окончательный выбор решения всегда определяется волевым актом «командира» (так можно условно назвать ответственное за выбор лицо). Дело исследователя — предоставить в распоряжение командира данные, помогающие ему делать выбор не «вслепую», а с учетом преимуществ и недостатков каждого варианта решения 1).
* * *
В заключение скажем несколько слов о так называемом «системном подходе» к. задачам выбора решений.
В настоящее время в связи с ростом масштабов и сложности операций все чаще приходится решать задачи оптимального управления так называемыми «сложными системами», включающими большое число элементов и подсистем и организованными обычно по иерархическому принципу. Например, какая-то отрасль народного хозяйства включает относительно самостоятельные специализированные управления, которые, в свою очередь, имеют в своем подчинении предприятия (фабрики, заводы); каждое предприятие включает подразделения, цеха и проч.
Оптимизируя (с точки зрения какого- либо критерия) работу одного звена сложной системы, нельзя забывать о связях, имеющихся между разными звеньями системы, между разными уровнями иерархии. Нельзя вырывать из цепи одно звено и рассматривать его, забывая об остальных.
1) Читателя, интересующегося многокритериальными задачами, отошлем к специальному руководству [3].
Простейший пример: пусть, оптимизируя работу заводского цеха, мы добились резкого увеличения объема продукции — это хорошо. Но готовые изделия скапливаются (в лучшем случае — на складах, а в худшем — во дворе), а транспортные средства не готовы к вывозу всей этой продукции. Такая ситуация может привести к материальным потерям, сводящим на нет выигрыш за счет увеличения продукции.
Другой пример: стремясь к перевыполнению плана по «валу», фабрика в огромном количестве выпускает изделия, не пользующиеся спросом, быстро переходящие в разряд «уцененных», что, разумеется, тоже ведет к потерям. Все это — результат «несистемного», «локального» планирования.
Какой из этого выход? Разумеется, не в жестком планировании работы всей огромной системы, когда в верхнем звене управления планируется все без исключения, вплоть до гвоздя, забитого в доску в каждом цехе. Это не только невозможно — к этому не надо и стремиться. Разумное управление сложной иерархической системой состоит в том, чтобы каждое вышестоящее звено давало задания нижестоящим не жестко регламентирование, а «в общих чертах», предоставляя им известную инициативу, но, так ставя перед ними цели, чтобы каждое звено, стремясь к своей цели, работало вместе с тем в согласии с интересами вышестоящего звена и системы в целом.
Это, разумеется, легче сказать, чем сделать. Математическая теория больших иерархических систем в настоящее время еще только разрабатывается. Создается математический аппарат, пригодный для описания таких систем, разрабатываются приемы «декомпозиции» больших систем на более удобные в рассмотрении «небольшие» элементы, но действенных методов управления такими системами пока не создано.
На практике «системный подход» в исследовании операций сводится пока что к тому, что каждое звено, работа которого оптимизируется, полезно рассмотреть как часть другой, более обширной системы, и выяснить, как влияет работа данного звена на работу последней.
ГЛАВА 3 ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
§ 7. Задачи линейного программирования
В предыдущих главах мы занимались только методологией исследования операций — классификацией задач, подходами к их решению и т. д., оставляя в стороне математический аппарат. В этой и последующих главах мы бегло рассмотрим некоторые из математических методов, широко применяемых в исследовании операций. В подробности этих методов не будем входить (научиться их применять по этой книжке нельзя);
главное внимание обратим на их принципиальные основы.
Выше мы уже упоминали о самых простых задачах, где выбор показателя эффективности (целевой функции) W достаточно явно диктуется целевой направленностью операции, а ее условия известны заранее (детерминированный случай). Тогда показатель эффективности зависит только от двух групп параметров: заданных условий а и элементов решения х, т. е.
W=W (a, x). (7.1)
Напомним, что в числе заданных условий ос фигурируют и ограничения, налагаемые на элементы решения. Пусть решение х
представляет собой совокупность п
элементов решения х1, x2, ..., xn (иначе — n-мерный вектор):
x = (x1, x2, …, xn ).
Требуется найти такие значения х1, х2, ..., xn, которые обращают величину W в максимум или в минимум (оба слова в математике объединяются под одним термином «экстремум»).
Такие задачи — отыскания значений параметров, обеспечивающих экстремум функции при наличии ограничений, наложенных на аргументы, носят общее название задач математического программирования 1).
Трудности, возникающие при решении задач математического программирования, зависят: а) от вида функциональной зависимости, связывающей W
с элементами решения, б) от «размерности» задачи, т. е. от количества элементов решения х1, х2, ..., xn, и в) от вида и количества ограничений, наложенных на элементы решения.
1) Слово «программирование» заимствовано из зарубежной литературы и попросту означает «планирование».
Среди задач математического программирования самыми простыми (и лучше всего изученными) являются так называемые задачи линейного программирования. Характерно для них то, что: а) показатель эффективности (целевая функция) W линейно зависит от элементов решения х1, х2, ..., xn и б) ограничения, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно х1, х2, ..., xn.
Такие задачи довольно часто встречаются на практике, например, при решении проблем, связанных с распределением ресурсов, планированием производства, организацией работы транспорта и т. д. Это и естественно, так как во многих задачах практики «расходы» и «доходы» линейно зависят от количества закупленных или утилизированных средств (например, суммарная стоимость партии товаров линейно зависит от количества закупленных; единиц; оплата перевозок производится пропорционально весам перевозимых грузов и т. д.).
Разумеется, нельзя считать, что все встречающиеся на практике типы зависимостей линейны; можно ограничиться более скромным утверждением, что линейные (и близкие к линейным) зависимости встречаются часто, а это уже много значит.
Приведем несколько примеров задач линейного программирования.
1. Задача о пищевом рационе. Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов:
П1, П2, П3, П4; стоимость единицы каждого продукта равна соответственно с1, с2, с3,, с4. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков — не менее b1 единиц; углеводов — не менее b2 единиц; жиров — не менее b3 единиц. Для продуктов П1, П2, П3, П4 содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице 7.1, где aij (i==1, 2, 3, 4; j=1, 2, 3) — какие-то определенные числа; первый индекс указывает номер продукта, второй — номер элемента (белки, углеводы, жиры)1).
Требуется составить такой пищевой рацион (т. е. назначить количества продуктов П1, П2, П3, П4, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.
Таблица 7.1
Продукт |
Элементы |
||
|
белки |
углеводы |
Жиры |
|
|
П1 П2 П3 П4 |
а11 а21 а31 а41 |
а12 а22 а32 а42 |
а13 а23 а33 а43 |
L = c1x1+c2x2+c3x3+c4x4,
или, короче,
L =

Итак, вид целевой функции известен и она линейна. Запишем теперь в виде формул ограничительные условия по белкам, углеводам и жирам. Учитывая, что в одной единице продукта П1 содержится а11
единиц белка, в х1
единицах—а11 х1
единиц белка, в х2
единицах продукта П2 содержится а21
х2 единиц белка и т. д., получим три неравенства:

Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения x1, x2, x3, x4,.
1) Разумеется, мы могли бы для «оживления» материала задать как числа b1, b2, b3,, так и числа аij вполне конкретными значениями, но это все равно не создало бы у читателя впечатления, что автор — специалист по откорму скота.
Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных х1, x2, x3, x4, чтобы они удовлетворяли ограничениям — неравенствам (7.3) и одновременно обращали в минимум линейную функцию этих переменных:
L ==

Перед нами — типичная задача линейного программирования. Не останавливаясь покуда на способах ее решения, приведем еще три примера аналогичных задач.
Таблица 7.2
Сырьё |
Изделия |
||
|
U1 |
U2 |
U3 |
|
|
s1 s2 s3 s4 |
а11 а12 а13 а14 |
а21 а22 а23 а24 |
а31 а32 а33 а34 |
2. Задача о планировании производства. Предприятие производит изделия трех видов: U1, U2, U3. По каждому виду изделия предприятию спущен план, по которому оно обязано выпустить не менее b1 единиц изделия
U1, не менее b2 единиц изделия U2 и не менее b3 единиц изделия U3. План может быть перевыполнен, но в определенных границах; условия спроса ограничивают количества произведенных единиц каждого типа: не более соответственно


При реализации одно изделие U1 приносит предприятию прибыль c1, U2 — прибыль c2, U3 — прибыль c3. Требуется так спланировать производство (сколько каких изделий производить), чтобы план был выполнен или перевыполнен (но при отсутствии «затоваривания»), а суммарная прибыль обращалась в максимум.
Запишем задачу в форме задачи линейного программирования. Элементами решения будут x1, x2, x3, — количества единиц изделий U1, U2, U3, которые мы произведем. Обязательность выполнения планового задания запишется в виде трех ограничений-неравенств:
x1 .



Отсутствие излишней продукции (затоваривания) даст нам еще три ограничения-неравенства:

Кроме того, нам должно хватить сырья. Соответственно четырем видам сырья будем иметь четыре ограничения-неравенства:

Прибыль, приносимая планом (x1, x2, x3) ,
будет равна
L = c1x1 + c2x2 + c3x3. (7.7)
Таким образом, мы снова получили задачу линейного программирования: найти (подобрать) такие неотрицательные значения переменных x1, x2, x3, чтобы они удовлетворяли неравенствам-ограничениям (7.4), (7.5), (7.6) и, вместе с тем, обращали в максимум линейную функцию этих переменных:
L = c1x1 + c2x2 + c3x3 => max. (7.8)
Задача очень похожа на предыдущую, разница в том, что неравенств-ограничений здесь больше и вместо «минимума» стоит «максимум» (а мы уже знаем, что это несущественно).
В следующей задаче мы уже встретимся с другого вида ограничениями.
3. Задача о загрузке оборудования. Ткацкая фабрика располагает двумя видами станков, из них N1 станков типа 1 и N2 станков типа 2. Станки могут производить три вида тканей: Т1, Т2, Т3, но с разной производительностью. Данные я„ производительности станков даны в таблице 7.3 (первый индекс — тип станка, второй — вид ткани).
Каждый метр ткани вида Т1 приносит фабрике доход с1, вида Т2 – доход с2, Т3 – доход с3.
Фабрике предписан план, согласно которому она должна производить в месяц не менее b1 метров ткани Т1, b2 метров ткани Т2, b3 метров ткани Т3; количество метров каждого вида ткани не должно превышать соответственно

Таблица 7.3
|
Тип станка |
Вид ткани |
||
|
Т1 |
Т2 |
Т3 |
|
|
1 2 |
а11 а21 |
а12 а22 |
а13 а23 |
в плане и максимизировать суммарный доход с1
х1 + c2x2 + c3x3. Но не торопитесь и спросите себя:
а где же тут возможности оборудования? Поразмыслив, мы увидим, что в этой задаче элементы решения — не количества тканей каждого вида, а количества станков типов 1 и 2, занятых производством тканей каждого вида. Здесь удобно обозначить элементы решения буквами х с двумя индексами (первый — тип станка, второй — вид ткани). Всего будет шесть элементов решения:

Здесь x11 — количество станков типа 1, занятых изготовлением ткани Т1, x12 — количество станков типа 1, занятых изготовленном ткани Т2,
и т. д.
Перед нами — еще одна задача линейного программирования. Запишем сначала условия-ограничения, наложенные на элементы решения хij. Прежде всего обеспечим выполнение плана. Это даст нам три неравенства-ограничения:

После этого ограничим перевыполнение плана; это даст нам еще три неравенства-ограничения:

Теперь запишем ограничения, связанные с наличием оборудования и его полной загрузкой. Суммарное количество станков типа 1, занятых изготовлением всех тканей, должно быть равно N1; типа 2 — N2. Отсюда еще два условия — на этот раз равенства:

Теперь запишем суммарный доход от производства всех видов тканей. Суммарное количество метров ткани T1, произведенное всеми станками, будет равно a11x11 + a21x21 .и принесет доход с1 (а11 х11 + а21
х21). Рассуждая аналогично, найдем суммарный доход фабрики за месяц при плане (7.9):
L = c1 (a11x11
+ a21x21 ) + c2 (a12x12
+ a22x22) + c3 (a13x13 + a23x23),
или, гораздо короче,
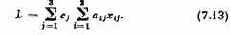
Эту линейную функцию шести аргументов мы хотим обратить в максимум:
L => max.
Перед нами — опять задача линейного программирования: найти такие неотрицательные значения переменных x11, x12, ..., x23, которые, во-первых, удовлетворяли бы ограничениям-неравенствам (7.10), (7.11), во-вторых — ограничениям-равенствам (7.12) и, наконец, обращали бы в максимум линейную функцию этих переменных (7.13). В этой задаче линейного программирования шесть ограничений-неравенств и два ограничения-равенства.
4. Задача о снабжении сырьем. Имеются три промышленных предприятия: П1, П2, П3, требующих снабжения определенным видом сырья. Потребности в сырье каждого предприятия равны соответственно а1, а2, а3
единиц. Имеются пять сырьевых баз, расположенных от предприятий па каких-то расстояниях и связанных с ними путями сообщения с разными тарифами. Единица сырья, получаемая предприятием Пi с базы Бj обходится предприятию в cij рублей (первый индекс — номер предприятия, второй — номер базы, см.
таблицу 7.4).
Таблица 7.4
Предприятие |
База |
||||
|
Б1 |
Б2 |
Б3 |
Б4 |
Б5 |
|
|
П1 П2 П3 |
с11 с21 с31 |
с12 с22 с32 |
с13 с23 с33 |
с14 с24 с34 |
с15 с25 с35 |
Опять поставим задачу линейного программирования. Обозначим хij количество сырья, получаемое i-м предприятием с j-и базы. Всего план будет состоять из 15 элементов решения:
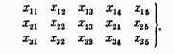
Введем ограничения по потребностям. Они состоят в том, что каждое предприятие получит нужное ему количество сырья (ровно столько, сколько ему требуется):

Далее напишем ограничения-неравенства, вытекающие из производственных мощностей баз:

Наконец, запишем суммарные расходы на сырье, которые мы хотим минимизировать. С учетом данных табл. 7.4 получим (пользуясь знаком двойной суммы):
L =

Опять перед нами задача линейного программирования: найти такие неотрицательные значения переменных xij которые удовлетворяли бы ограничениям-равенствам (7.15), ограничениям-неравенствам (7.16) и обращали бы в минимум их линейную функцию (7.17).
Таким образом, мы рассмотрели несколько задач линейного программирования. Все они сходны между собой, разнятся только том, что в одних требуется обратить линейную функцию в максимум, в других — в минимум; в одних ограничения — только неравенства, в других — как равенства, так и неравенства. Бывают задачи линейного программирования, где все ограничения — равенства. Эти различия несущественны, так как от ограничений-неравенств легко переходить к ограничениям-равенствам и обратно, как будет показано в следующем параграфе.
§ 8. Основная задача линейного программирования
Любую задачу линейного программирования можно свести к стандартной форме, так называемой «основной задаче линейного программирования» (ОЗЛП), которая формулируется так: найти неотрицательные значения переменных х1, х2, ..., xn, которые удовлетворяли бы условиям-равенствам
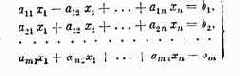
и обращали бы в максимум линейную функцию этих переменных:
L = c1x1 + c2x2 + ... + cnxn =>max. (8.2)
Убедимся в этом. Uo-нерпых, случай, когда L
надо обратить не в максимум, а и минимум, легко сводится к предыдущему, если попросту изменить знак L на обратный (максимизировать не L, а L' = — L). Кроме того, от любых условий-неравенств можно перейти к условиям-равенствам ценой введения некоторых новых «дополнительных» переменных. Покажем, как это делается, на конкретном примере.
Пусть требуется найти неотрицательные значения переменных х1, х2, х3, удовлетворяющие ограничениям-неравенствам

и обращающие в максимум линейную функцию от этих переменных:
L = 4х1 – х2
+ 2х3 => max. (8.4)
Начнем с того, что приведем условия (8.3) к стандартной форме, так, чтобы знак неравенства был


А теперь обозначим левые части неравенств (8.5) соответственно через у1 и у2:

Из условий (8.5) и (8.6) видно, что новые переменные у1, у2 также должны быть неотрицательными.
Какая же теперь перед нами стоит задача? Найти неотрицательные значения переменных х1, х2, х3, y1, у2 такие, чтобы они удовлетворяли условиям-равенствам (8.6) и обращали в максимум линейную функцию этих переменных (то, что в L не входят дополнительные переменные у1, у2, неважно: можно считать, что они входят, но с нулевыми коэффициентами). Перед нами — основная задача линейного программирования (ОЗЛП). Переход к ней от первоначальной задачи с ограничениями-неравенствами (8.3) «куплен» ценой увеличения числа переменных на два (число неравенств).
Возможен и обратный переход: от ОЗЛП к задаче с ограничениями-неравенствами. Пусть перед нами основная задача линейного программирования с ограничениями-равенствами (8.1). Предположим, что среди этих т
равенств линейно независимыми являются r

переменных x1, x2, ..., xn, равно п, так что вообще r

= п - r. При этом надо будет освободить от базисных переменных также и функцию L, подставив в нее их выражения через свободные. Таким образом, при переходе от ОЗЛП к задаче с ограничениями-неравенствами число переменных не увеличивается, а уменьшается на число г независимых условий-равенств в ОЗЛП. Примеров такого перехода мы приводить не будем, предоставляя пытливому читателю самому убедиться в его возможности.
Итак, всякая задача линейного программирования может быть сведена к стандартной форме ОЗЛП. Мы не будем подробно останавливаться на способах решения этой задачи. Им посвящены специальные руководства (например, [4, 5]), они описаны во многих книгах по исследованию операций (например, [6, 7]). В следующем параграфе мы изложим только некоторые соображения общего характера относительно существования решения ОЗЛП и способов его нахождения.
Никакими расчетными алгоритмами мы заниматься не будем, а отошлем интересующегося читателя к вышеупомянутым руководствам.
1) Равенства называются линейно независимыми, если никакое из них нельзя получить из других путем умножения на какие-то коэффициенты и суммирования, т. е. никакое из них не является следствием остальных.)
§ 9. Существование решения ОЗЛП в способы его нахождения
Рассмотрим основную задачу линейного программирования (ОЗЛП): найти неотрицательные значения переменных х1, x2, ..., хn, удовлетворяющие т условиям-равенствам:

и обращающие в максимум линейную функцию этих переменных:
L = с1х1
+ с2х2 + … + сnxn => max. (9.2)
Для простоты предположим, что все условия (9.1) линейно независимы (r = m), и будем вести рассуждения в этом предположении 1).
Назовем допустимым решением ОЗЛП всякую совокупность неотрицательных значений х1, х2,..., xn, удовлетворяющую условиям (9.1). Оптимальным назовем то из допустимых решений, которое обращает в максимум функцию (9.2). Требуется найти оптимальное решение.
Всегда ли эта задача имеет решение? Нет, не всегда. Во-первых, может оказаться, что уравнения (9.1) вообще несовместны (противоречат друг другу).
1) Если среди условий-равенств (9.1) есть некоторые лишние, вытекающие из других, то это обнаружится автоматически в процессе решения ОЗЛП (см. [4, 6]).
Может оказаться и так, что они совместны, но не в области неотрицательных решений, т. е. не существует ни одной совокупности чисел х1



 |
2). Такой частный случай дает возможность геометрической интерпретации ОЗЛП па плоскости.
Мы знаем, что т линейно независимых уравнении (9.1) всегда можно разрешить относительно каких-то т базисных переменных, выразив их через остальные, свободные, число которых равно п - т = k (в нашем случае k = 2). Предположим, что свободные переменные — это х1 и х2 (если это не так, то всегда можно заново перенумеровать переменные), а остальные: х3, х4,..., хn—базисные. Тогда вместо т уравнений (9.1) мы получим тоже т уравнений, но записанных в другой форме, разрешенных относительно х3, х4,...:
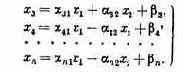
Будем изображать пару значений свободных переменных точкой с координатами х1, х2 (рис. 9.1). Так как переменные х1, х2 должны быть неотрицательными, то допустимые значения свободных переменных лежат только выше оси Ox1 (на которой х2 = 0) и правее оси Ох2 (на которой х1
= 0). Это мы отметим штриховкой, обозначающей «допустимую» сторону каждой оси.
Теперь построим па плоскости х10х2
область допустимых решений или же убедимся, что ее не существует. Базисные переменные х3,x4, ..., xn тоже должны быть неотрицательными и удовлетворять уравнениям (9.3). Каждое такое уравнение ограничивает область допустимых решений. Действительно, положим
в первом уравнении (9.3) х3 = 0; получим уравнение прямой линии:

На этой прямой х3 =0; по одну сторону от нее х3 >0, по другую — х3
< 0. Отметим штриховкой ту сторону (полуплоскость), где х3 > 0 (рис. 9.2). Пусть эта сторона оказалась правее и выше прямой х3
= 0. Значит, вся область допустимых решений (ОДР) лежит в первом координатном угле, правее и выше прямой х3
= 0. Аналогично поступим и со всеми остальными условиями (9.3). Каждое из них изобразится прямой со штриховкой, указывающей «допустил1ую» полуплоскость, где только и может лежать решение (рис. 9.3).
Таким образом, мы построили п
прямых: две оси координат {Ox1
и Ox2) и п — 2 прямых х3 =
0, х4 = 0,..., хn = 0. Каждая из них определяет «допустимую» полуплоскость, где может лежать решение. Часть первого координатного угла, принадлежащая одновременно всем этим полуплоскостям, и есть ОДР. На рис. 9.3 показан случай, когда ОДР существует, т. е. система уравнений (9.3) имеет неотрицательные решения, Заметим, что этих решении— бесконечное множество, так как любая пара значений свободных переменных, взятая из ОДР, «годится», а из х1 и х2
могут быть определены и базисные переменные.
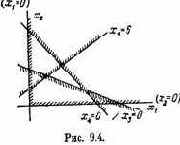 |
Предположим, что область допустимых решений существует, и мы ее построили. Как же теперь найти среди них оптимальное?
Для этого дадим геометрическую интерпретацию условию (9.2)
L => max. Подставив выражения (9.3) в формулу (9.2), выразим L через свободные переменные х1, x2. После приведения подобных членов получим:
L=

где



х2, он мог и появиться. Однако мы его тут же и отбросим: ведь максимум линейной функции L достигается при тех же значениях х1, х2, что и максимум линейной однородной функции (без свободного члена):
L’ =

Посмотрим, как изобразить геометрически условие L’ =>
шах. Положим сначала L’ = 0, т.е.

прямую с таким уравнением; очевидно, он проходит через начало координат (рис. 9.5). Назовем ее «опорной прямой». Если мы будем придавать L’ какие-то значения С1, С2, С3,...,
прямая будет перемещаться параллельно самой себе; при перемещении в одну сторону L’ будет возрастать, в другую — убывать.
Отметим на рис. 9.5 стрелками, поставленными у опорной прямой, то направление, в котором L'
возрастает. На рис. 9.5 это оказалось направление «направо — вверх», но могло быть и наоборот: все зависит от коэффициентов

L’ достигнет максимума? Очевидно, в точке А (крайней точке ОДР в направлении стрелок). В этой точке свободные переменные принимают оптимальные значения


 |
 |
На рис. 9.6 оптимальное решение существовало и было единственным. А сейчас рассмотрим случай, когда
оптимальное решение существует, но не единственно (их бесконечное множество).
1) Если бы стрелки были направлены иначе («налево — вниз»), то крайней точкой ОДР в направлении стрелок была бы точка В.
Это случай, когда максимум L’ достигается не в одной точке А, а на целом отрезке АВ,
параллельном опорной прямой (рис. 9.8). Такой случай встречается на практике, но нас он
 |
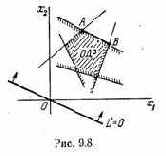 |
безразлично), и в поисках оптимального решения можно ограничиться вершинами ОДР.
Итак, мы рассмотрели в геометрической интерпретации случай п - т = k=2 и убедились в следующем: оптимальное решение (если оно существует) всегда достигается в одной из вершин ОДР, в точке, где по крайней мере две из переменных х1, х2,..., хn равны нулю.
Оказывается, аналогичное правило справедливо и в случае n - m = k > 2 (только геометрическая интерпретация теряет в этом случае свою наглядность). Обойдемся без доказательства, просто сформулируем это правило.
Оптимальное решение ОЗЛП (если оно существует) достигается при такой совокупности значений переменных х1, х2,..., хn, где по крайней мере k из них обращаются в нуль, а остальные неотрицательны.
При k = 2 такая совокупность значений изображается точкой на плоскости, лежащей в одной из вершин многоугольника допустимых решений (ОДР). При k =
3 ОДР представляет собой уже не многоугольник, а многогранник, и оптимальное решение достигается в одной из его вершин. При k
> 3 геометрическая интерпретация теряет наглядность, но все же геометрическая терминология остается удобной. Мы будем продолжать говорить о «многограннике допустимых решений» в k-мерном пространстве, а оптимальное решение (если оно существует) будет достигаться в одной из вершин этого многогранника, где, по крайней мере, k
переменных равны нулю, а остальные — неотрицательны. Будем для краткости называть такую вершину «опорной точкой», а вытекающее из нее решение — «опорным решением».
Отсюда вытекает идея, лежащая в основе большинства рабочих методов решения ОЗЛП,— идея «последовательных проб». Действительно, попробуем разрешить уравнения (9.1) относительно каких-нибудь m
базисных переменных и выразим их через остальные k свободных. Попробуем положить эти свободные переменные равными нулю — авось повезет, наткнемся на опорную точку. Вычислим базисные переменные при нулевых значениях свободных. Если все они оказались неотрицательными, значит, нам повезло, мы сразу же получим допустимое (опорное) решение, и его остается только оптимизировать. А если нет? Значит, данный выбор свободных и базисных переменных допустимого решения не дает; точка лежит не на границе, а вне ОДР. Что делать? Надо «переразрешить» уравнения относительно каких-то других базисных переменных, но не как попало, а так, чтобы это приближало нас к области допустимых решений (для этого в линейном программировании существуют специальные приемы, на которых мы останавливаться не будем).
Пусть, наконец, несколько раз повторив такую процедуру, мы нашли опорное решение ОЗЛП. Браво! Но это еще не все. Тут надо поставить вопрос: а является ли это решение оптимальным? Выразим функцию L
через последние получившиеся свободные переменные и попробуем увеличивать их сверх нуля. Если от этого значение L
только уменьшается, значит, нам повезло, и мы нашли оптимальное решение, ОЗЛП решена. А если нет? Снова «пере разрешаем» систему уравнений относительно других базисных переменных, и снова не как попало, а так, чтобы, не выходя за пределы допустимых решений, приблизиться к оптимальному. И опять-таки для этого в линейном программировании существуют специальные приемы, гарантирующие, что при каждом новом «пере разрешении» мы будем приближаться к оптимальному решению, а не удаляться от него. На этих приемах мы тоже здесь не будем останавливаться. После конечного числа таких шагов цель будет достигнута — оптимальное решение найдено. А если его не существует? Алгоритм решения ОЗЛП сам покажет вам, что решения нет.
Читатель, может быть, спросит: только-то и всего? Зачем было придумывать хитрые методы решения ОЗЛП, может быть, надо просто перебрать, одну за другой, все возможные комбинации k свободных переменных, полагая их равными нулю, пока, наконец, не будет найдено оптимальное решение?
Действительно, для простых задач, где число переменных невелико, такой «слепой перебор» может привести к решению, и довольно быстро. Но на практике часто встречаются задачи, в которых число переменных (и наложенных условий) очень велико, порядка сотен и даже тысяч. Для таких задач простой перебор становится практически невозможным: слишком велико число комбинаций свободных и базисных переменных. Пример: только при п = 30 и m = 10 число возможных комбинаций свободных переменных с базисными равно

Разработанные в теории линейного программирования вычислительные методы («симплекс-метод», «двойственный симплекс-метод» и другие, см. [4,6,8]) позволяют находить оптимальное решение не «слепым» перебором, а «целенаправленным», с постоянным приближением к решению.
Добавим, что современные ЭВМ, как правило, снабжены подпрограммами для решения задач линейного программирования, так что лицу, желающему их решать, нет даже особой надобности обучаться решению таких задач «вручную» — труд крайне неприятный и изнурительный.
§ 10. Транспортная задача линейного программирования
В предыдущем параграфе мы описали некоторые общие подходы к решению задач линейного программирования. Однако существуют частные типы задач линейного программирования, которые, в силу особой своей структуры, допускают решение более простыми методами. Из них мы остановимся только на одной — так называемой «транспортной задаче» (ТЗ). Она ставится следующим образом: имеются т
пунктов отправления (ПО) A1, А2., ..., An, в которых сосредоточены запасы каких-то однородных грузов в количестве соответственно a1, a2, ..., am единиц. Имеются п пунктов назначения (ПН) В1, В2,..., Вn, подавших заявки соответственно на b1, b2, ..., bn единиц груза. Сумма всех заявок равна сумме всех запасов:
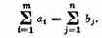
Известны стоимости cij перевозки единицы груза от каждого пункта отправления Ai до каждого пункта назначения Вj (i=l, 2,..., т; j=1,
2,..., n). Все числа су, образующие прямоугольную таблицу (матрицу), заданы:

Коротко матрицу (10.2) будем обозначать (cij).
Считается, что стоимость перевозки нескольких единиц груза пропорциональна их числу.
Требуется составить такой план перевозок (откуда, куда и сколько единиц везти), чтобы все заявки были выполнены, а общая стоимость всех перевозок минимальна.
Поставим эту задачу как задачу линейного программирования. Обозначим xij, — количество единиц груза, отправляемого из i-го ПО Ai в j-и ПН Bj. Неотрицательные переменные xij тоже можно записать в виде матрицы
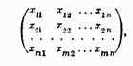
которую мы будем коротко обозначать (хij). Совокупность чисел (хij) (10.3) мы будем называть «планом перевозок», а сами величины хij — «перевозками». Эти неотрицательные переменные должны удовлетворять следующим условиям.
1. Суммарное количество груза, направляемого из каждого ПО во все ПН, должно быть равно запасу груза в данном пункте. Это даст нам т условий-равенств:

2. Суммарное количество груза, доставляемого в каждый ПН из всех ПО, должно быть равно заявке, поданной данным пунктом. Это даст нам п условий-равенств:

3. Суммарная стоимость всех перевозок, то есть сумма величин хij, умноженных на соответствующие стоимости cij, должна быть минимальной:
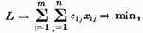
где знак двойной суммы означает, что суммирование производится по всем комбинациям индексов i и j, т. е. но всем парам ПО — ПН.
Мы видим, что перед нами — задача линейного программирования с условиями-равенствами (10.4), (10.5) и минимизируемой линейной функцией (10.6). Особенностью этой задачи является то, что все коэффициенты в условиях (10.4), (10.5) равны единице — это позволяет решать задачу очень простыми способами. О них и пойдет речь.
Прежде всего, замечаем, что условия-равенства (10.4), (10.5) не являются линейно независимыми, так как их правые части связаны условием (10.1). Число линейно независимых среди уравнений (10.4), (10.5) равно не m + n (числу уравнений), а т + п — 1. Общее число переменных xij в нашей задаче равно т • п; как бы ни разрешать уравнения (10.4), (10.5), число базисных переменных будет равно т + п — 1, а число свободных переменных
k = тп – (т + п - 1) = (т - 1) (n - 1).
Мы знаем, что в задаче линейного программирования оптимальное решение достигается в одной из вершин ОДР, в опорной точке, где по крайней мере k переменных равны нулю. Значит, в пашем случае для оптимального плана по крайней мере (m - 1) (n - 1) перевозок должны быть равны нулю (из соответствующих ПО в соответствующие ПН ничего не перевозится).
Будем называть любой план перевозок допустимым, если он удовлетворяет условиям (10.4), (10.5) (все заявки удовлетворены, все запасы исчерпаны). Допустимый план будем называть опорным, если в нем отличны от нуля не более т + п -
1 базисных перевозок, а остальные перевозки равны нулю. План (хij) будем называть оптимальным, если он, среди всех допустимых планов, приводит к минимальной суммарной стоимости перевозок (L = min).
В силу особой структуры ТЗ при ее решении не приходится долго и нудно разрешать и пере разрешать систему уравнений. Все операции по нахождению оптимального плана сводятся к манипуляциям непосредственно с таблицей, где в определенном порядке записаны условия транспортной задачи: перечень ПО и ПН, заявки и запасы, а также стоимости перевозок сij. По мере заполнения этой таблицы в ее клетках проставляются сами перевозки xij. Транспортная таблица состоит из т строк и п столбцов. В правом верхнем углу каждой клетки мы будем ставить стоимость сij перевозки единицы груза из Аi в Bj, а центр клетки оставим свободным, чтобы помещать в нее саму перевозку xij. Клетку таблицы, соответствующую пунктам Аi Вj будем кратко обозначать (i, j).
Пример транспортной таблицы, где приведены условия задачи и стоимости перевозок, по нет еще самих перевозок, дан в таблице 10.1, где т = 4, п = 5.
Прежде всего займемся составлением опорного плана.. Это в транспортной задаче очень просто: можно, например, применить так называемый «метод северо-западного угла». Продемонстрируем его непосредственно на конкретных данных таблицы 10.1. Начнем заполнение транспортной таблицы с левого верхнего («северо-западного») угла. Пункт В1 подал заявку на 18 единиц груза; удовлетворим ее из запасов пункта
Таблица 10.1
 по |
В1 |
В2 |
В3 |
В4 |
В5 |
Запасы аi |
A1 |
13 |
7 |
14 |
7 |
5 |
30 |
|
A2 |
11 |
8 |
12 |
6 |
8 |
48 |
|
A3 |
6 |
10 |
10 |
8 |
11 |
20 |
|
A4 |
14 |
8 |
10 |
10 |
15 |
30 |
|
Заявки bj |
18 |
27 |
42 |
15 |
26 |
128 |
Проверим, является ли этот план допустимым: да, потому что в нем сумма перевозок по строке равна запасу соответствующего пункта отправления, а сумма перевозок по столбцу — заявке соответствующего пункта назначения; значит, все в порядке — все заявки удовлетворены, все запасы израсходованы (сумма запасов равна сумме заявок и выражается числом 128, стоящим в правом нижнем углу таблицы).
Здесь и в дальнейшем мы проставляем в таблице только отличные от нуля перевозки, а клетки, соответствующие нулевым перевозкам, оставляем «свободными». Проверим, является ли план перевозок, данный в таблице 10.2, опорным (не слишком ли много там отличных от нуля, «базисных» перевозок?). Число свободных клеток с нулевыми перевозками в таблице 10.2 равно как раз (m-1)(n-1) = 3•4 = 12, так что план — опорный. Вот как нам его удалось легко построить!

|
Пн по |
В1 |
В2 |
В3 |
В4 |
В5 |
Запасы аi |
|
A1 |
13 18 |
7 12 |
14 |
7 |
5 |
30 |
|
A2 |
11 |
8 15 |
12 33 |
6 |
8 |
48 |
|
A3 |
6 |
10 |
10 9 |
8 11 |
11 |
20 |
|
A4 |
14 |
8 |
10 |
10 4 |
15 26 |
30 |
|
Заявки bj |
18 |
27 |
42 |
15 |
26 |
128 |
Очевидно, в результате циклического переноса допустимый план остается допустимым — баланс запасов и заявок не нарушается. Ну что же, произведем этот перенос и запишем новый, улучшенный план перевозок в таблице 10.3.
Теперь посмотрим, чего мы добились, сколько сэкономили? Общая стоимость плана, показанного в таблице 10.2, равна L1 = 18 • 13 + 12 • 7 + 15 • 8+33 • 12 + +9 • 10+11-8+4-10+26-15 =1442;
Таблица 10.3
|
ПН ПО |
В1 |
В2 |
В3 |
В4 |
В5 |
Запасы аi |
|
А1 |
18 13 |
12 7 |
14 |
7 |
5 |
30 |
|
А2 |
11 |
15 8 |
22 12 |
11 6 |
8 |
48 |
|
А3 |
6 |
10 |
20 10 |
8 |
11 |
20 |
|
А4 |
14 |
8 |
10 |
4 10 |
26 15 |
30 |
|
Заявки bj |
18 |
27 |
42 |
15 |
26 |
128 |
Таким образом, нам удалось уменьшить стоимость перевозок на 1442 — 1398 = 44 единицы. Это, впрочем, можно было предсказать и не подсчитывая полную стоимость плана. Действительно, алгебраическая сумма стоимостей, стоящих в вершинах цикла, со знаком плюс, если перевозки в этой вершине увеличиваются, и со знаком минус — если уменьшаются (так называемая «цена цикла»), в данном случае равна: 6 - 8+10 - 12 = - 4. Значит, при переносе одной единицы груза по этому циклу стоимость перевозок уменьшается на четыре. А мы их перенесли целых 11; значит, стоимость должна была уменьшиться на 11•4 = 44 единицы, что и произошло.
Значит, весь секрет оптимизации плана перевозок в том, чтобы переносить («перебрасывать») перевозки по циклам, имеющим отрицательную цену.
В теории линейного программирования доказывается, что при опорном плане для каждой свободной клетки транспортной таблицы существует цикл, и притом единственный, одна вершина которого (первая) лежите данной свободной клетке, а остальные — в базисных клетках. Поэтому, отыскивая «выгодные» циклы с отрицательной ценой, мы должны высматривать — нет ли в таблице соблазнительных, «дешевых» свободных клеток.
Если такая клетка есть, нужно для нее найти цикл, вычислить его цену и, если она будет отрицательной, перенести по этому циклу столько единиц груза, сколько будет возможно (без того, чтобы какие-то перевозки сделать отрицательными). При этом данная свободная клетка становится базисной, а какая-то из бывших базисных — свободной. Очевидно, это равносильно «переразрешению» системы уравнений относительно других базисных переменных, по делается это гораздо легче.
Попробуем еще раз улучшить план, приведенный и таблице 10.3. Например, нас «соблазняет» дешевая клетка (1.5) со стоимостью 5. Нельзя ли улучшить план, увеличив перевозки в этой клетке, зато, уменьшив в других (при этом, конечно, придется кое-где перевозки тоже увеличить). Давайте разглядим внимательно таблицу 10.3 и найдем в пей цикл, первая вершина которого лежит в свободной клетке (1.5), а остальные — все в базисных клетках.' Немного подумав, мы этот цикл обнаружим: это последовательность клеток (1.5)





Подсчитаем цену этого цикла. Она равна 5 – 15 + 10 – 6 + 8 - 7= - 5. Так как цена цикла отрицатель-па, то переброска перевозок по этому циклу выгодна. Посмотрим, сколько же единиц мы можем по нему перебросить? Это определяется наименьшей перевозкой, стоящей в отрицательной вершине цикла. В данном случае это опять 11 (чистое совпадение!). Умножая 11 па цепу цикла — 5 получим, что за счет переброски 11 единиц груза по данному циклу мы еще уменьшим стоимость перевозок на 55 (предоставляем любознательному читателю сделать это самостоятельно).
Таким образом, разыскивая в транспортной таблице свободные клетки с отрицательной ценой цикла и перебрасывая по этому циклу наибольшее возможное количество груза, мы будем все уменьшать и уменьшать стоимость перевозок.
Бесконечно уменьшаться она не может (она никак не может стать меньше нуля!), значит, рано или поздно мы придем к оптимальному плану. Для такого плана уже не остается ни одной свободной клетки с отрицательной ценой цикла. Это — признак того, что оптимальное решение найдено.
Таблица 10.4
 ПО |
B1 |
B2 |
B3 |
B4 |
B5 |
Запасы аi |
|
A1 |
13 18 |
7  |
14 |
7 |
5 |
30 |
|
A2 |
11 |
8 |
12 22 |
6 11  |
8 |
48 |
|
A3 |
6 |
10 |
10 20 |
8 |
11 |
20 |
|
A4 |
14 |
8 |
10 |
10 |
15 -26 |
30 |
|
Заявки bj |
18 |
27 |
42 |
15 |
26 |
128 |
В заключение скажем несколько слов о так называемой «транспортной задаче с неправильным балансом», когда сумма заявок не равна сумме запасов:
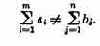
Если

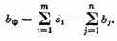
Тогда задача сводится к задаче с правильным балансом, так как
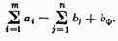
Возникает вопрос: а каковы же стоимости перевозок из пунктов отправления Ai в «фиктивный» пункт назначения Bф? Естественно положить их равными нулю (ведь фактически в пункт Вф
ничего перевозиться не будет!). Поэтому для любого пункта отправления стоимость сiф = 0.
Введем в транспортную таблицу дополнительный столбец, соответствующий пункту назначения Вф, и проставим в нем нулевые стоимости перевозок. После этого задача решается как обычная транспортная, и для нее находится оптимальный план перевозок:
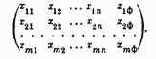
При этом нужно иметь в виду, что все перевозки хiф, стоящие в правом столбце, фактически никуда не отправляются, а остаются на пунктах отправления Ai.
Может встретиться также случай 

(запасов не хватает для удовлетворения всех заявок);
в этом случае можно тем или другим способом «срезать» заявки и снова получить транспортную задачу с правильным балансом. Если нас совершенно не интересует, насколько «справедливо» удовлетворяются заявки, а важно только «подешевле развезти» имеющиеся запасы (все равно, куда), то можно ввести в рассмотрение фиктивный пункт отправления Аф, условно приписав ему недостающий запас, равный

Подробнее на этих вопросах мы останавливаться не будем (см. [6]).
§ 11. Задачи целочисленного программирования. Понятие о нелинейном программировании
На практике часто встречаются задачи, совпадающие по постановке с задачами линейного программирования, по отличающиеся тон особенностью, что искомые значения переменных непременно должны быть целым и. Такие задачи называются задачами целочисленного программирования; дополнительное условие целочисленности переменных существенно затрудняет их решение.
Рассмотрим пример такой задачи. Пусть имеется ряд предметов (ценностей) П1, П2, … Пn, которые желательно увезти из угрожаемого района. Известны стоимости этих предметов: с1, с2, ..., сn и их веса q1, q2, …, qn Количество и вид предметов, которые мы можем увезти, лимитируется грузоподъемностью Q машины. Требуется из всего набора предметов выбрать наиболее ценный набор (с максимальной суммарной стоимостью предметов), вес которого укладывается в Q.
Введем в рассмотрение переменные х1, х2, ..., xn, определяемые условием: xi =1, если мы берём в машину предмет Пi и xi = 0,— если не берем.
При заданных значениях х1, х2, ..., xn суммарный вес предметов, которые мы берем в машину, равен q1x1 + q2x2 + ... + qnxn. Условие ограниченной грузоподъемности запишется в виде неравенства:
q1x1
+ q2x2 +.... + qnxn

Теперь запишем общую стоимость предметов, которую мы хотим максимизировать:
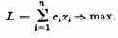
Таким образом, задача на вид почти не отличается от обычной задачи линейного программирования: найти неотрицательные значения переменных х1, х2, ..., хn, которые удовлетворяют неравенству (11.1) и обращают в максимум линейную функцию этих переменных (11.2). На первый взгляд может показаться, что и решать ее надо как задачу линейного программирования, введя дополнительные ограничения-неравенства (каждый предмет — только один!):
x1



Ничуть не бывало! Найденное таким образом решение может оказаться не целым, а дробным, а значит неосуществимым (не можем же мы погрузить в машину треть рояля и половину шкафа!). Наша задача отличается от обычной задачи линейного программирования: она представляет собой задачу целочисленного программирования.
Вторая мысль, которая приходит в голову: а нельзя ли решить обычную задачу линейного программирования и округлить полученные значения хi до ближайшего из целых чисел 0 или 1? К сожалению, и так в общем случае поступать нельзя. Полученное таким образом решение даже может не удовлетворять ограничению (11.1), т. е. «не влезет» в данный вес Q. А если и «влезет», то может быть совсем не оптимальным. В отдельных случаях такое округление допустимо; например, если мы в задаче 3 § 7 получим ответ:
«производством ткани первого вида надо занять 185,3 станков первого типа», то, разумеется, мы без зазрения совести округлим это решение до 185. Если же идет речь о ресурсах неделимых (особо ценных или же уникальных), то задачу надо ставить как задачу целочисленного программирования.
Надо заметить, что вообще задачи целочисленного программирования гораздо труднее, чем обычные задачи линейного программирования.
На практике применяется ряд методов решения подобных задач; все они (при сколько-нибудь значительном числе переменных) очень сложны и трудоемки. Мы не будем пытаться излагать эти методы здесь, а отошлем интересующегося читателя к более подробным руководствам (например, [7, 8]).
В заключение скажем несколько слов о задачах нелинейного программирования.
Общая постановка задачи нелинейного программирования следующая. Найти неотрицательные значения переменных х1, х2, ..., xn, удовлетворяющие каким-то ограничениям произвольного вида. Например
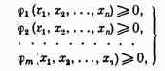
и обращающие в максимум произвольную нелинейную функцию этих переменных:
W = W (x1, х2, ..., хn) => mах. (11.4)
Общих способов решения задачи нелинейного программирования не существует; в каждой конкретной задаче способ выбирается в зависимости от вида функции W и накладываемых на элементы решения ограничений.
Задачи нелинейного программирования на практике возникают довольно часто, например, когда затраты растут не пропорционально количеству закупленных или произведенных товаров (эффект «оптовости»), но многие нелинейные задачи могут быть приближенно заменены линейными (линеаризованы), по крайней мере в области, близкой к оптимальному решению. Если это и невозможно, все же обычно нелинейные задачи, возникающие на практике, приводят к сравнительно «благополучным» формам нелинейности. В частности, нередко встречаются задачи «квадратичного программирования», когда W есть полином 2-й степени относительно переменных х1, x2, ..., хn, а неравенства (11.3) линейны (см. [7, 8]). В ряде случаев при решении задач нелинейного программирования может быть с успехом применен так называемый «метод штрафных функций», сводящий задачу поиска экстремума при наличии ограничений к аналогичной задаче при отсутствии ограничений, которая обычно решается проще. Идея метода состоит в том, что вместо того, чтобы наложить на решение жесткое требование вида

..., xn)


Далее можно, увеличивая абсолютное значение a, посмотреть, как изменяется при этом оптимальное решение (

В последнюю очередь упомянем о так называемых задачах стохастического программирования. Особенность их в том, что ищется оптимальное решение в условиях неполной определенности, когда ряд параметров, входящих в целевую функцию W, и ограничения, накладываемые на решение, представляют собой случайные величины. Такое программирование называется стохастическим. Существуют задачи, где стохастическое программирование сводится к обычному, детерминированному. Например, когда оптимизация производится «в среднем», целевая функция W линейно зависит от элементов решения, случайны только коэффициенты при элементах решения, а накладываемые условия не содержат случайности. Тогда можно оптимизировать решение, забыв о случайном характере коэффициентов и заменив их математическими ожиданиями (ибо, как вы знаете, математическое ожидание линейной функции равно той же линейной функции от математических ожиданий аргументов). Гораздо более серьезен случай, когда на элементы решения накладываются стохастические ограничения. Проблемы стохастического программирования довольно полно освещены в монографии [31].
В отличие от задач линейного программирования, методы, решения которых хорошо отлажены, устоялись и не представляют существенных трудностей, задачи целочисленного, нелинейного и особенно стохастического программирования принадлежат к сложным и трудным вычислительным задачам. При их решении часто приходится прибегать к приближенным, так называемым «эвристическим» методам оптимизации, так как точные методы, но своей трудоемкости оказываются неподъемными даже для современной вычислительной техники.
Бывает так, что весь выигрыш, который был бы получен от точной оптимизации решения, «съедается» затратами на получение этого решения, так что «игра не стоит свеч». Здесь опять мы встречаемся с необходимостью «системного» подхода к задачам исследования операций, учета не только непосредственного выигрыша в данной операции, по и затрат па со оптимизацию.
Правда, возможности вычислительной техники (быстродействие, объем памяти) с точением времени растут, и то, что невыгодно экономически сегодня, может сделаться выгодным завтра. С другой стороны, параллельно с ростом возможностей вычислительной техники растет и сложность оптимизационных задач, которые приходится решать. Не надо забывать, что принятие того или иного способа оптимизации решения есть тоже «решение», и иной раз весьма ответственное.
ГЛАВА 4
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
§ 12. Метод динамического программирования
Динамическое программирование (иначе «динамическое планирование») есть особый метод оптимизации решений, специально приспособленный к так называемым «многошаговым» (пли «многоэтапным») операциям.
Представим себе некоторую операцию O,
распадающуюся на ряд последовательных «шагов» или «этапов»,— например, деятельность отрасли промышленности в течение ряда хозяйственных лет; или же преодоление группой самолетов нескольких полос противовоздушной обороны; или же последовательность тестов, применяемых при контроле аппаратуры. Некоторые операции (подобно выше приведенным) расчленяются на шаги естественно; в некоторых членение приходится вводить искусственно — скажем, процесс наведения ракеты на цель можно условно разбить на этапы, каждый из которых занимает какое-то время

Итак, рассмотрим операцию O, состоящую из т шагов (этапов). Пусть эффективность операции характеризуется каким-то показателем W, который мы для краткости будем в этой главе называть «выигрышем». Предположим, что выигрыш W за всю операцию складывается из выигрышей на отдельных шагах:
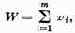
где wi — выигрыш на i-м шаге.
Если W обладает таким свойством, то его называют «аддитивным критерием».
Операция О, о которой идет речь, представляет собой управляемый процесс, т. е. мы можем выбирать какие-то параметры, влияющие на его ход и исход, причем на каждом шаге выбирается какое-то решение, от которого зависит выигрыш на данном шаге и выигрыш за операцию в целом. Будем называть это решение «шаговым управлением». Совокупность всех шаговых управлений представляет собой управление операцией в целом. Обозначим его буквой х, а шаговые управления — буквами х1, х2, ..., xm:
x = (x1, x2, …, xm). (12.2)
Следует иметь в виду, что х1, х2,
...., xm в общем случае — не числа, а, может быть, векторы, функции и т. д.
Требуется найти такое управление х, при котором выигрыш W обращается в максимум:
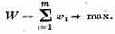
То управление х*, при котором этот максимум достигается, будем называть оптимальным управлением. Оно состоит из совокупности оптимальных шаговых управлений:
х* =(

Тот максимальный выигрыш, который достигается при этом управлении, мы будем обозначать W*:
W* =

Формула (12.5) читается так: величина W* есть максимум из всех W{x} при разных управлениях х (максимум берется по всем управлениям х, возможным в данных условиях). Иногда это последнее оговаривается в формуле и пишут:
 |
1. Планируется деятельность группы промышленных предприятий П1, П2, ..., Пk на период т
хозяйственных лет (m-летку). В начале периода на развитие группы выделены какие-то средства М, которые должны быть как-то распределены между предприятиями. В процессе работы предприятия, вложенные в него средства частично расходуются (амортизируются), а частично сохраняются и снова могут быть перераспределены.
Каждое предприятие за год приносит доход, зависящий от того, сколько средств в него вложено. В начале каждого хозяйственного года имеющиеся в наличии средства перераспределяются между предприятиями. Ставится вопрос: какое количество средств в начале каждого года нужно выделять каждому предприятию, чтобы суммарный доход за т лет был максимальным?
Выигрыш W (суммарный доход) представляет собой сумму доходов на отдельных шагах (годах):
и, значит, обладает свойством аддитивности.
Управление xi на i-м шаге состоит в том, что в начале i-го года предприятиям выделяются какие-то средства хi1, хi2, ..., хik (первый индекс — номер шага, второй — номер предприятия). Таким образом, шаговое управление есть вектор с k составляющими:
xi = (xi1, xi2, …, xik). (12.7)
Разумеется, величины wi в формуле (12.6) зависят от количества вложенных в предприятия средств.
Управление х всей операцией состоит из совокупности всех шаговых управлений:
x
= (x1, x2, ..., xm ). (12.8)
Требуется найти такое распределение средств по предприятиям и по годам (оптимальное управление x*), при котором величина W обращается в максимум.
В этом примере шаговые управления были векторами; в последующих примерах они будут проще и выражаться просто числами.
2. Космическая ракета состоит из т ступеней, а процесс ее вывода на орбиту — из m этапов, в конце каждого из которых очередная ступень сбрасывается. На все ступени (без учета «полезного» веса кабины) выделен какой-то общий вес:
G = G1
+ G2 + … + Gm,
где gi — вес i-й ступени.
В результате i-го этапа (сгорания и сбрасывания 1-й ступени) ракета получает приращение скорости

В данном случае показатель эффективности (выигрыш) будет
V =

где

х = (Gi, Gi, ..., Gm).
Оптимальным управлением х* будет то распределение весов по ступеням, при котором скорость V максимальна. В этом примере шаговое управление — одно число, а именно, вес данной ступени.
3. Владелец автомашины эксплуатирует ее в течение т лет. В начале каждого года он может принять одно из трех решений:
1) продать машину и заменить ее новой;
2) ремонтировать ее и продолжать эксплуатацию;
3) продолжать эксплуатацию без ремонта.
Шаговое управление — выбор одного из этих трех решений. Непосредственно числами они не выражаются, но можно приписать первому численное значение 1, второму 2, третьему 3. Какие нужно принять решения по годам (т. е. как чередовать управления 1, 2, 3), чтобы суммарные расходы на эксплуатацию, ремонт и приобретение новых машин были минимальны?
Показатель эффективности (в данном случае это не «выигрыш», а «проигрыш», но это неважно) равен
W =

где wi — расходы в i-м году. Величину W требуется обратить в минимум.
Управление операцией в целом представляет собой какую-то комбинацию чисел 1, 2, 3, например:
x = (3, 3, 2, 2, 2, 1, 3, ...),
что означает: первые два года эксплуатировать машину без ремонта, последующие три года ее ремонтировать, в начале шестого года продать, купить новую, затем снова эксплуатировать без ремонта и т. д. Любое управление представляет собой вектор (совокупность чисел):
х = (j1, j2, …; jm), (12.11)
где каждое из чисел j1, j2, ..., jm имеет одно из трех значений: 1, 2 или 3. Нужно выбрать совокупность чисел (12.11), при которой величина (12.10) минимальна.
4. Прокладывается участок железнодорожного пути между пунктами А и В (рис. 12.1). Местность пересеченная, включает лесистые зоны, холмы, болота, реку, через которую надо строить мост.
Требуется так провести дорогу из А и В,
чтобы суммарные затраты на сооружение участка были минимальны.
В этой задаче, в отлично от трех предыдущих, нет естественного членения на шаги: его приходится вводить искусственно, для чего, например, можно отрезок АВ разделить на т частей, провести через точки деления прямые, перпендикулярные АВ, и считать за «шаг» переход с одной такой прямой на другую. Если провести их достаточно близко друг от друга, то можно считать на каждом шаге участок пути прямолинейным. Шаговое управление на г-м шаге представляет собой угол

х = (

Требуется выбрать такое (оптимальное) управление х*, при котором суммарные затраты па сооружение всех участков минимальны:
W =

Итак, мы рассмотрели несколько примеров многошаговых задач исследования операций. А теперь поговорим о том, как можно решать подобного рода задачи?
Любую многошаговую задачу можно решать по-разному: либо искать сразу все элементы решения на всех m шагах, либо же строить оптимальное управление шаг за шагом, па каждом этапе расчета оптимизируя только один шаг. Обычно второй способ оптимизации оказывается проще, чем первый, особенно при большом числе шагов.
Такая идея постепенной, пошаговой оптимизации и лежит в основе метода динамического программирования. Оптимизация одного шага, как правило, проще оптимизации всего процесса: лучше, оказывается, много раз решить сравнительно простую задачу, чем один раз — сложную.
С первого взгляда идея может показаться довольно тривиальной. В самом деле, чего казалось бы, проще:
если трудно оптимизировать операцию в целом, разбить ее на ряд шагов. Каждый такой шаг будет отдельной, маленькой операцией, оптимизировать которую уже нетрудно. Надо выбрать на этом шаге такое управление, чтобы эффективность этого шага была максимальна. Не так ли?
Нет, вовсе не так! Принцип динамического программирования отнюдь не предполагает, что каждый шаг оптимизируется отдельно, независимо от других.
Напротив, шаговое управление должно выбираться дальновидно, с учетом всех его последствий в будущем. Что толку, если мы выберем на данном шаге управление, при котором эффективность этого шага максимальна, если этот шаг лишит нас возможности хорошо выиграть на последующих шагах?
Пусть, например, планируется работа группы промышленных предприятий, из которых часть занята выпуском предметов потребления, а остальные производят для них машины. Задача операции — получить за т лет максимальный объем выпуска предметов потребления. Допустим, планируются капиталовложения на первый год. Исходя из узких интересов этого шага (года), мы должны были бы все наличные средства вложить в производство предметов потребления. Но правильно ли будет такое решение с точки зрения эффективности операции в целом? Очевидно, нет. Это решение — расточительное, недальновидное. Имея в виду будущее, надо выделить какую-то долю средств и на производство машин. От этого объем продукции за первый год, конечно, снизится, зато будут созданы условия для его увеличения в последующие годы.
Еще пример. Допустим, что в задаче 4 (прокладка железнодорожного пути из А
в В) мы прельстимся идеей сразу же устремиться по самому легкому (дешевому) направлению. Что толку от экономии на первом шаге, если в дальнейшем он заведет нас (буквально или фигурально) в «болото»?
Значит, планируя многошаговую операцию, надо выбирать управление на каждом шаге с учетом всех его будущих последствий на еще предстоящих шагах. Управление на i-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален, а так, чтобы была максимальна сумма выигрышей на всех оставшихся до конца шагах плюс данный.
Однако из этого правила есть исключение. Среди всех шагов есть один, который может планироваться попросту, без оглядки на будущее. Какой это шаг? Очевидно, последний! Этот шаг, единственный из всех, можно планировать так, чтобы он сам, как таковой, принес наибольшую выгоду.
Поэтому процесс динамического программирования обычно разворачивается от конца к началу: прежде всего, планируется последний, m-й шаг.
А как его спланировать, если мы не знаем, чем кончился предпоследний? Т. е. не знаем условий, в которых мы приступаем к последнему шагу?
Вот тут-то и начинается самое главное. Планируя последний шаг, нужно сделать разные предположения о том, чем кончился предпоследний, (т -
1)-й шаг, и для каждого из этих предположений найти условное оптимальное управление на m-м шаге («условное» потому, что оно выбирается исходя из условия, что предпоследний шаг кончился так-то и так-то).
Предположим, что мы это сделали, и для каждого из возможных исходов предпоследнего шага знаем условное оптимальное управление и соответствующий ему условный оптимальный выигрыш на m-м шаге. Отлично! Теперь мы можем оптимизировать управление на предпоследнем, (т-1)-м шаге. Снова сделаем все возможные предположения о том, чем кончился предыдущий, (m
- 2)-й шаг, и для каждого из этих предположений найдем такое управление на (m- 1)-м шаге, при котором выигрыш за последние два шага (из которых m-й уже оптимизирован!) максимален. Так мы найдем для каждого исхода (m - 2)- шага условное оптимальное управление на (т - 1)-м шаге и условный оптимальный выигрыш на двух последних шагах. Далее, «пятясь назад», оптимизируем управление на (m
- 2)-м шаге и т. д., пока не дойдем до первого.
Предположим, что все условные оптимальные управления и условные оптимальные выигрыши за весь «хвост» процесса (на всех шагах, начиная от данного и до конца) нам известны. Это значит: мы знаем, что надо делать, как управлять на данном шаге и что мы за это получим на «хвосте», в каком бы состоянии ни был процесс к началу шага. Теперь мы можем построить уже не условно оптимальное, а просто оптимальное управление х* и найти не условно оптимальный, а просто оптимальный выигрыш W*.
В самом деле, пусть мы знаем, в каком состоянии S0 была управляемая система (объект управления S) в начале первого шага. Тогда мы можем выбрать оптимальное управление


Тогда нам тоже известно условное оптимальное управление

которое к концу второго шага переводит систему в состояние

Таким образом, в процессе оптимизации управления методом динамического программирования многошаговый процесс «проходится» дважды: первый раз — от конца к началу, в результате чего находятся условные оптимальные управления и условные оптимальные выигрыши за оставшийся «хвост» процесса; второй раз — от начала к концу, когда нам остается только «прочитать» уже готовые рекомендации и найти безусловное оптимальное управление х*,
состоящее из оптимальных шаговых управлений

Первый этап — условной оптимизации — несравненно сложнее и длительнее второго. Второй этап почти не требует дополнительных вычислений.
Автор не льстит себя надеждой, что из такого описания метода динамического программирования читатель, не встречавшийся с ним до сих пор, поймет по-настоящему его идею. Истинное понимание возникает при рассмотрении конкретных примеров, к которым мы и перейдем.
§ 13. Примеры решения задач динамического программирования
В этом параграфе мы рассмотрим (и даже решим до конца) несколько простых (до крайности упрощенных) примеров задач динамического программирования
1. Прокладка наивыгоднейшего пути между двумя пунктами. Вспомним задачу 4 предыдущего параграфа и решим ее до конца в крайне (и намеренно) упрощенных условиях. Нам нужно соорудить путь, соединяющий

Рис. 13.1.
два пункта А и В, из которых второй лежит к северо-востоку от первого. Для простоты допустим,. что прокладка пути состоит из ряда шагов, и на каждом шаге мы можем двигаться либо строго на восток, либо строго на север; любой путь из А
в В представляет собой ступенчатую ломаную линию, отрезки которой параллельны одной из координатных осей (рис. 13.1). Затраты на сооружение каждого из таких отрезков известны. Требуется проложить такой путь из А
в В, при котором суммарные затраты минимальны.
Как это сделать? Можно поступить одним из двух способов: либо перебрать все возможные варианты пути, и выбрать тот, на котором затраты минимальны (а при большом числе отрезков это очень и очень трудно!); либо разделить процесс перехода из А в В
на отдельные шаги (один шаг — один отрезок) и оптимизировать управление по шагам. Оказывается, второй способ несравненно удобнее! Тут, как и везде в исследовании операций, сказываются преимущества целенаправленного, организованного поиска решения перед наивным «слепым» перебором.
Продемонстрируем, как это делается, на конкретном примере. Разделим расстояние от А до В
в восточном направлении, скажем, на 7 частей, а в северном — на 5 частей (в принципе дробление может быть сколь угодно мелким). Тогда любой путь из А в В
состоит из т = 7 + 5 == 12 отрезков, направленных на восток или на север (рис. 13.2). Проставим на каждом из отрезков число, выражающее (в каких-то условных единицах) стоимость прокладки пути по этому отрезку. Требуется выбрать такой путь из А в В,
для которого сумма чисел, стоящих на отрезках, минимальна.
Будем рассматривать сооружаемый путь как управляемую систему S, перемещающуюся под влиянием управления из начального состояния А в конечное В. Состояние этой системы перед началом каждого шага будет характеризоваться двумя координатами: восточной (х) и северной (у), обе — целочисленные (0





Процедуру условной оптимизации будем разворачивать в обратном направлении — от конца к началу.
Прежде всего произведем условную оптимизацию последнего, 12-го шага. Рассмотрим отдельно правый верхний угол нашей прямоугольной сетки (рис. 13.3). Где мы можем находиться после 11-го шага? Только
 |
















там, откуда за один (последний) шаг можно попасть в В,
т. е. в одной из точек В1
или В2. Если мы находимся в точке В1,
у нас нет выбора (управление вынужденное): надо идти на восток, и это обойдется нам в 10 единиц. Запишем это число 10 в кружке у точки В1, а оптимальное управление покажем короткой стрелкой, исходящей из В1
и направленной на восток. Для точки В2
управление тоже вынужденное (север), расход до конца равен 14, мы его запишем в кружке у точки В2.
Таким образом, условная оптимизация последнего шага сделана, и условный оптимальный выигрыш для каждой из точек В1, В2 найден и записан в соответствующем кружке.
Теперь давайте оптимизировать предпоследний (11-й) шаг. После предпредпоследнего (10-го) шага мы могли оказаться в одной из точек С1, С2, С3 (рис. 13.4). Найдем для каждой из них условное оптимальное управление и условный оптимальный выигрыш. Для точки С1 управление вынужденное: идти на восток;
обойдется это нам до конца в 21 единицу (11 на данном шаге, плюс 10, записанных в кружке при В1). Число 21 записываем в кружке при точке С1. Для точки С2 управление уже не вынужденное: мы можем идти как на восток, так и на север. В первом случае мы затратим на данном шаге 14 единиц и от В2 до конца — еще 14, всего 28 единиц. Если пойдем на север, затратим 13 + 10, всего 23 единицы. Значит, условное оптимальное управление в точке С2
— идти на север (отмечаем это стрелкой, а число 23 записываем в кружке у С2), Для точки С3 управление снова вынужденное («с»), обойдется это до конца в 22 единицы (ставим стрелку на север, число 22 записываем в кружке при С3).

• Рис. 13.5.
Аналогично, «пятясь» от предпоследнего шага назад, найдем для каждой точки с целочисленными координатами условное оптимальное управление («с» или «в»), которое обозначим стрелкой, и условный оптимальный выигрыш (расход до конца пути), который запишем в кружке. Вычисляется он так: расход на данном шаге складывается с уже оптимизированным расходом, записанным в кружке, куда ведет стрелка. Таким образом, на каждом шаге мы оптимизируем только этот шаг, а следующие за ним — уже оптимизированы. Конечный результат процедуры оптимизации показан на рис. 13.5.
Таким образом, условная оптимизация уже выполнена: в какой бы из узловых точек мы ни находились, мы уже знаем, куда идти (стрелка) и во что нам обойдется путь до конца (число в кружке). В кружке при точке А
записан оптимальный выигрыш на все сооружение пути из А в В:
W* = 118.
Теперь остается построить безусловное оптимальное управление — траекторию, ведущую из А и В самым дешевым способом. Для этого нужно только «слушаться стрелок», т. е. прочитать, что они предписывают делать на каждом шаге. Такая оптимальная траектория отмечена на рис. 13.5 дважды обведенными кружками. Соответствующее безусловное оптимальное управление будет:
х* = (с, с, с, с, в, в, с, в, в, в, в, в),
т. е. первые четыре шага мы должны делать на север, следующие два — на восток, затем опять один на север и остальные пять — на восток. Задача решена.
Заметим, что в ходе условной оптимизации мы можем столкнуться со случаем, когда оба управления для какой-то точки на плоскости являются оптимальными, т. е. приводят к одинаковому расходу средств от этой точки до конца, Например, в точке с координатами (5; 1) оба управления «с» и «в» являются оптимальными и дают расход до конца равным 62. Из них мы произвольно выбираем любое (в нашем случае мы выбрали «с»; с тем же успехом мы могли бы выбрать «в»). Такие случаи неоднозначного выбора оптимального управления постоянно встречаются в динамическом программировании; в дальнейшем мы специально отмечать их не будем, а попросту выберем произвольно любой из равноценных вариантов.
От этого произвола, разумеется, может зависеть оптимальное управление всем процессом, но не оптимальный выигрыш. Вообще, в задачах динамического программирования (как и в задачах линейного) решение далеко не всегда единственное.
А теперь вернемся к началу и попробуем решить задачу «наивным» способом, выбирая на каждом шаге, начиная с первого, самое выгодное (для этого шага) направление (если таких два, выбираем любое). Таким способом мы получим управление
х = (с, с, в, в, в, в, с, в, в, в, с, с).
Подсчитаем расходы для этой траектории. Они будут равны W
=10 +12 +8+10 +11 +13 +15+8 + +10+9+8+14=128, что безусловно больше, чем W* = 118. В данном случае разница не очень велика, но в других она может быть существенной.
В решенной выше задаче условия были намеренно до крайности упрощены. Разумеется, никто не будет вести железнодорожный путь «по ступенькам», перемещаясь только строго на север или строго на восток. Такое упрощение мы сделали для того, чтобы в каждой точке выбирать только из двух управлений: «с» или «в». Можно было бы вместо двух возможных направлений ввести их несколько и, кроме того, взять шаги помельче; принципиального значения это не имеет, но, разумеется, усложняет и удлиняет расчеты.
Заметим, что задачи, сходные с рассмотренной выше, очень часто встречаются на практике: например, при выборе наискорейшего пути между двумя точками или наиболее экономного (в смысле расхода горючего) набора скорости и высоты летательным аппаратом.
Сделаем одно попутное замечание. Внимательный читатель, вероятно, заметил, что в нашей задаче точки А и В (начало и конец) в принципе ничем друг от друга не отличаются: можно было бы строить условные оптимальные управления не с конца к началу, а с начала к концу, а безусловные — в обратном направлении. Действительно, это так: в любой задаче динамического программирования «начало» и «конец» можно поменять местами. Это совершенно равносильно описанной ранее методике в расчетном отношении, но несколько менее удобно при словесном объяснении идеи метода: легче аргументировать, ссылаясь на «уже сложившиеся» условия к началу данного шага, чем на те, которые еще «предстоят» после этого шага.
По существу же оба подхода совершенно равносильны.
2. Задача о распределении ресурсов. Метод динамического программирования позволяет с успехом решать многие экономические задачи (см., например, [6, 10]). Рассмотрим одну из простейших таких задач. В нашем распоряжении имеется какой-то запас средств (ресурсов) К, который должен быть распределен между т предприятиями П1, П2, ..., Пm. Каждое из предприятий Пi при вложении в него каких-то средств х приносит доход, зависящий от x, т. е. представляющий собой какую-то функцию


заданы (разумеется, эти функции — неубывающие). Спрашивается, как нужно распределить средства К. между предприятиями, чтобы в сумме они дали максимальный доход?
Эта задача легко решается методом динамического программирования.. Хотя в своей постановке она не содержит упоминания о времени, можно все же операцию распределения средств мысленно развернуть в какой-то последовательности, считая за первый шаг вложение средств в предприятие П1, за второй — в П2
и т. д.
Управляемая система S в данном случае — средства или ресурсы, которые распределяются. Состояние системы S перед каждым шагом характеризуется одним числом S — наличным запасом еще не вложенных средств. В этой задаче «шаговыми управлениями» являются средства х1, х2, ..., х3,
выделяемые предприятиям. Требуется найти оптимальное управление, т. е. такую совокупность чисел х1, х2,
..., хm, при которой суммарный доход максимален:
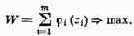
Решим эту задачу сначала в общем, формульном виде, а потом — для конкретных числовых данных. Найдем для каждого i-го шага условный оптимальный выигрыш (от этого шага и до конца), если мы подошли к данному шагу с запасом средств S. Обозначим условный оптимальный выигрыш Wi(S), а соответствующее ему условное оптимальное управление — средства, вкладываемые в i-е предприятие, — xi(S).
Начнем оптимизацию с последнего, т - го шага. Пусть мы подошли к этому шагу с остатком средств S. Что нам делать? Очевидно, вложить всю сумму S целиком в предприятие Пm.
Поэтому условное оптимальное управление на m-м шаге: отдать последнему предприятию все имеющиеся средства S, т. е.
xm(S)=S,
а условный оптимальный выигрыш
Wm
(S)=

Задаваясь целой гаммой значений S
(располагая их достаточно тесно), мы для каждого значения S будем знать xm(S) и Wm(S). Последний шаг оптимизирован.
Перейдем к предпоследнему, (т— 1)-му шагу. Пусть мы подошли к нему с запасом средств S. Обозначим Wm-1(S) условный оптимальный выигрыш на двух последних шагах: (m - 1)-м и m-м (который уже оптимизирован). Если мы выделим на (m - 1)-м шаге (m - 1)-му предприятию средства х, то на последний шаг останется S — х. Наш выигрыш на двух последних шагах будет равен

и нужно найти такое х, при котором этот выигрыш максимален:

Знак

Далее оптимизируем (т—2)-й, (т—3)-й и т. д. шаги. Вообще, для любого i-го шага будем находить условный оптимальный выигрыш за все шаги с этого и до конца по формуле

и соответствующее ему условное оптимальное управление xi(S) — то значение х, при котором этот максимум достигается.
Продолжая таким образом, дойдем, наконец, до 1-го предприятия П1. Здесь нам не нужно будет варьировать значения S;
мы точно знаем, что запас средств перед первым шагом равен К:

Итак, максимальный выигрыш (доход) от всех предприятий найден. Теперь остается только «прочесть рекомендации». То значение х,
при котором достигается максимум (13.4), и есть оптимальное управление



и т. д. до конца.
А теперь решим численный пример. Исходный запас средств К = 10 (условных единиц), и требуется его оптимальным образом распределить между пятью предприятиями (т =
5). Для простоты предположим, что вкладываются только целые количества средств. Функции дохода

Таблица 13.1
|
х |
 |
 |
 |
 |
 |
|
1 2 3 4 5 6 7 8 |
0,5 1,0 1,4 2,0 2,5 2,8 3,0 3,0 |
0,1 0,5 1,2 1,8 2,5 2,9 3,5 3,5 |
0,6 1,1 1,2 1,4 1,6 1,7 1,8 1,8 |
0,3 0,6 1,3 1,4 1,5 1,5 1,5 1,5 |
1,0 1,2 1,3 1,3 1,3 1,3 1,3 1,3 |
Произведем условную оптимизацию так, как это было описано выше, начиная с последнего, 5-го шага. Каждый раз, когда мы подходим к очередному шагу, имея запас средств S, мы пробуем выделить па этот шаг то или другое количество средств, берем выигрыш па данном шаге по таблице 13.1, складываем с уже оптимизированным выигрышем на всех последующих шагах до конца (учитывая, что средств у нас осталось уже меньше, как раз на такое количество средств, которое мы выделили) и находим то вложение, на котором эта сумма достигает максимума. Это вложение и есть условное оптимальное управление на данном шаге, а сам максимум — условный оптимальный выигрыш.
В таблице 13.2 даны результаты условной оптимизации по всем шагам. Таблица построена так: в первом столбце даются значения запаса средств S, с которым мы подходим к данному шагу. Далее таблица разделена на пять пар столбцов, соответственно номеру шага. В первом столбце каждой пары приводится значение
Таблица 13.2
|
S |
i=5 |
i=4 |
i=3 |
i=2 |
i=1 |
|||||
|
x5(S) |
W5(S) |
x4(S) |
W4(S) |
x3(S) |
W3(S) |
x2(S) |
W2(S) |
x1(S) |
W1(S) |
|
|
1 2 3 4 5 6 7 8 9 10 |
1 2 3 4 5 6 7 8 9 10 |
1,0 1,2 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 |
0 1 2 3 3 4 5 5 6 7 |
1,0 1,3 1,6 2,3 2,5 2,6 2,7 2,8 2,8 2,8 |
0 1 2 2 1 2 2 4 5 5 |
1,0 1,6 2,1 2,4 2,9 3,4 3,6 3,7 3,9 4,1 |
0 0 0 0 0 5 5 5 7 7 |
1,0 1,6 2,1 2,4 2,9 3,5 4,1 4,6 5,1 5,6 |
2 |
5,6 |
условного оптимального управления, во втором — условного оптимального выигрыша. Таблица заполняется слева направо, сверху вниз. Решение на пятом — последнем — шаге вынужденное: выделяются все средства;
па всех остальных шагах решение приходится оптимизировать. В результате последовательной оптимизации 5-го, 4-го, 3-го, 2-го и 1-го шагов мы получим полный список всех рекомендаций по оптимальному управлению и безусловный оптимальный выигрыш W* за всю операцию — в данном случае он равен 5,6. В последних двух столбцах таблицы 13.2 заполнена только одна строка, так, как состояние системы перед началом первого шага нам в точности известно:
S0 = К = 10. Оптимальные управления на всех шагах выделены рамкой. Таким образом, мы получили окончательный вывод: надо выделить первому предприятию две единицы из десяти, второму — пять единиц, третьему — две, четвертому — ни одной, пятому — одну единицу. При этом распределении доход будет максимален и равен 5,6.
Чтобы читателю было понятно, как заполняется таблица 13.2, продемонстрируем это на одном образце расчета. Пусть, например, нам нужно оптимизировать решение х3(7)—как поступать на третьем шаге, если мы подошли к нему с запасом средств S = 7, и сколько максимум мы можем выиграть на всех оставшихся
Таблица 13.3
|
x |
7 - x |
 |
W4(7 - x) |
 |
|
7 6 5 4 3 1 0 |
0 1 2 3 4 5 6 7 |
1,8 1,7 1,6 1,4 1,2 1,1 0,6 0 |
0 1,0 1,3 1,6 2,3 2,5 2,6 2,7 |
1,8 2,7 2,9 3,0 3,5 3,2 2,7 |
Во втором столбце — то, что останется после такого вложения от запаса средств S = 7. В третьем столбце — выигрыш на третьем шаге от вложения средств х
в третье предприятие заполняется по столбцу (

Из всех выигрышей последнего столбца выбирается максимальный (в таблице 13.3 он равен W3(7) = 3,6, а соответствующее управление х(7) = 2).
Возникает вопрос: а что если во вспомогательной таблице типа 13.3 максимум достигается не при одном x, а при двух или больше? Отвечаем: совершенно все равно, какое из них выбрать; от этого выигрыш не зависит. Вообще, в задачах динамического программирования решение вовсе не должно быть единственным (мы об этом уже упоминали).
3. Задача о загрузке машины. Пользуясь методом динамического программирования, можно с успехом решать ряд задач оптимизации, описанных в главе 3, в частности, некоторые задачи целочисленного программирования. Заметим, что целочисленность решений, так затрудняющая задачи линейного программирования, в данном случае не усложняет, а наоборот, упрощает процедуру (как нам ее упростила целочисленность вложений в предыдущей задаче).
В качестве примера рассмотрим задачу о загрузке машины (мы уже упоминали о пей в предыдущей главе): имеется определенный набор предметов П1, П2,..., Пn (каждый в единственном экземпляре); известны их веса q1, q2, ..., qn и стоимости с1, с2, ..., сn. Грузоподъемность машины равна Q. Спрашивается, какие из предметов нужно взять в машину, чтобы их суммарная стоимость (при суммарном весе

Нетрудно заметить, что эта задача, в сущности, ничем не отличается от предыдущей (распределение ресурсов между п
предприятиями), но несколько проще со. В самом деле, процесс загрузки машины можно представлять себе как состоящий из п
шагов; на каждом шаге мы отвечаем па вопрос: брать данный предмет в машину или не брать? Управление на i - м шаге равно единице, если мы данный (i-я.) предмет берем, и пулю — если не берем.
Значит, па каждом шаге у пас всего два управления, а это очень приятно.
А чем мы будем характеризовать состояние системы S перед очередным шагом? Очевидно, весом S, который еще остался в нашем распоряжении до конца (полной загрузки машины) после того, как предыдущие шаги выполнены (какие-то предметы погружены в машину). Для каждого из значений S мы должны найти Wi (S) — суммарную максимальную стоимость предметов, которыми можно «догрузить» машину при данном значении S,
и положить xi (S) = 1, если мы данный (i-й) предмет берем в машину, и xi (S) = 0,если не берем. Затем эти условные рекомендация должны быть прочтены, и дело с концом!
Решим до конца конкретный числовой пример: имеется шесть предметов, веса и стоимости которых указаны в таблице 13.4.
Таблица 13.4
|
Предмет Пi |
П1 |
П2 |
П3 |
П4 |
П5 |
П6 |
|
Вес qi |
4 |
7 |
11 |
12 |
16 |
20 |
|
Стоимость ci |
7 |
10 |
15 |
20 |
27 |
34 |
Как и ранее, будем придавать S только целые значения. Условная оптимизация решения показана в таблице 13.5, где в каждой строке для соответствующего номера шага (номера предмета) приведены: условное оптимальное управление xi (0 или 1) и условный оптимальный выигрыш Wi (стоимость всех оставшихся до конца предметов при оптимальном управлении, но всех шагах). Как эта таблица составляется, мы уже объяснять не будем — тут полная аналогия с предыдущей задачей, с той разницей, что возможные управления только 0 или 1.
В таблице 13.5 выделены: оптимальный выигрыш W* = 57 и оптимальные шаговые управления, при которых этот выигрыш достигается:

т. е. загрузить машину надо предметами 2, 4 и 5, суммарный вес которых равен в точности 35 (вообще это необязательно; при оптимальном выборе грузов может быть и некоторый общий «недогруз»).
Заметим, что в нашем элементарном примере, возможно, было бы проще искать решение «простым перебором»), пробуя все возможные комбинации предметов, проверяя на каждой из них, «влезают» ли они в заданный вес, и выбирая ту, для которой стоимость максимальна.
Но при большом числе предметов это было бы затруднительно: число комбинаций неумеренно растет при увеличении числа предметов. Для метода же динамического программирования увеличение числа шагов не страшно: оно только приводит к пропорциональному возрастанию объема расчетов.
Таблица 13.5
|
S |
i=6 |
i=5 |
i=4 |
i=3 |
i=2 |
i=1 |
|||||||
|
xi |
Wi |
xi |
Wi |
xi |
Wi |
xi |
Wi |
xi |
Wi |
xi |
Wi |
||
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 |
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 34 34 34 34 34 34 34 34 34 34 34 34 34 34 34 34 |
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 27 27 27 27 34 34 34 34 34 34 34 34 34 34 34 34 34 34 34 34 |
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 |
0 0 0 0 0 0 0 0 0 0 0 0 20 20 20 20 27 27 27 27 34 34 34 35 35 35 35 42 47 47 47 49 54 54 54 54 |
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0 0 |
0 0 0 0 0 0 0 0 0 0 0 15 20 20 20 27 27 27 27 34 34 34 35 35 35 35 35 42 47 47 47 49 54 54 54 54 |
0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 |
0 0 0 0 0 0 0 10 10 10 10 15 20 20 20 20 27 27 27 30 34 34 34 37 37 37 37 44 47 47 47 49 54 54 54 54 |
0 |
57 |
|
1) Предметы в таблице 13.4 перенумерованы в порядке возрастания веса; стоимости их также возрастают, что не обязательно, но естественно. Заранее ясно, что загружать машину предметами большого веса и малой стоимости нецелесообразно.
§ 14. Задача динамического программирования в общем виде. Принцип оптимальности
Рассмотренные выше простейшие задачи динамического программирования дают понятие об общей идее метода: пошаговая оптимизация, проходимая в одном направлении «условно», в другом — «безусловно». Метод динамического программирования является очень мощным и плодотворным методом оптимизации управления; ему не страшны ни целочисленность решения, ни нелинейность целевой функции, ни вид ограничений, накладываемых на решение. Но в отличие от линейного программирования динамическое программирование не сводится к какой-либо стандартной вычислительной процедуре; оно может быть передано на машину только после того, как записаны соответствующие формулы, а это часто бывает не так-то легко.
В этом параграфе мы дадим нечто вроде «сводки советов начинающим» — как ставить задачи динамического программирования, в каком порядке их решать, как записывать и т. д.
Первый вопрос, на который нужно ответить ставящему задачу: какими параметрами характеризуется состояние управляемой системы S
перед каждым шагом? От удачного выбора набора этих параметров часто зависит возможность успешно решить задачу оптимизации. В трех конкретных примерах, которые мы решали в предыдущем параграфе, состояние системы характеризовалось очень небольшим числом параметров: двумя координатами — в первом примере, одним числом — во втором и третьем. Но такие ультрапростые задачи не так уже часто встречаются на практике. Если, как это обычно и бывает, состояние системы описывается многими параметрами (так называемыми «фазовыми координатами»), то становится трудно перед каждым шагом перебрать все их варианты и для каждого найти оптимальное условное управление. Последнее еще больше затрудняется в случае, когда число возможных вариантов управления велико.
В этих случаях над нами повисает, по меткому выражению Р. Беллмана, «проклятие многомерности» — бич не только метода динамического программирования, но и всех других методов оптимизации. Обычно задачи динамического программирования решаются не вручную, а на ЭВМ, однако многие такие задачи не под силу даже современным машинам. Поэтому очень важно уметь правильно и «скромно» поставить задачу, не переобременяя ее лишними подробностями, упрощая елико возможно описание управляемой системы и вариантов управления. Так что в методе динамического программирования очень многое зависит от искусства и опыта исследователя.
Вторая задача после описания системы и перечня управлений — это членение на шаги (этапы). Иногда (на счастье) оно бывает задано в самой постановке задачи (например, хозяйственные годы в экономических задачах), но часто членение на шаги приходится вводить искусственно как мы сделали, например, в задаче 1 § 13. Если бы мы в этой задаче не ограничились самым примитивным случаем всего двух управлений («с» и «в»), то было бы удобнее членение на шаг произвести иначе, например, считая за «шаг» переход с одной прямой, параллельной оси ординат, на другую. Можно было бы вместо прямых рассмотреть окружности с центром в точке А или же другие кривые. Все такие способы выбора наивыгоднейшего пути неизбежно ограничивают выбор возможных направлений. Если за «шаги» считать переходы с одной прямой, параллельной оси ординат, на другую, то здесь множество возможных управлений не предусматривает «пути назад», т. е. с более восточной прямой на более западную. В большинстве задач практики такие ограничения естественны (например, трудно себе представить, чтобы наивыгоднейшая траектория космической ракеты, пущенной с Земли, на каких-то участках включала движение «назад», ближе к Земле). Но бывает и другая обстановка. Например, путь по сильно пересеченной местности («серпантинная» дорога в горах) часто «петляет» и возвращается ближе к исходному пункту. При постановке задачи динамического программирования, в частности при выборе системы координат и способа членения на шаги, должны быть учтены все разумные ограничения, накладываемые на управление.
Как быть с числом шагов те? С первого взгляда может показаться, что чем больше т, тем лучше. Это не совсем так. При увеличении те возрастает объем расчетов, а это не всегда оправдано. Число шагов нужно выбирать с учетом двух обстоятельств: 1) шаг должен быть достаточно мелким для того, чтобы процедура оптимизации шагового управления была достаточно проста, и 2) шаг должен быть не слишком мелким, чтобы не производить ненужных расчетов, только усложняющих процедуру поиска оптимального решения, но не приводящих к существенному изменению оптимума целевой функции. В любом случае практики нас интересует не строго оптимальное, а «приемлемое» решение, не слишком отличающееся от оптимального по значению выигрыша W*.
Сформулируем общий принцип, лежащий в основе решения всех задач динамического программирования (его часто называют «принципом оптимальности»):
Каково бы ни было состояние системы S перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.
По-видимому, полное понимание этого принципа делается возможным (для лиц с обычным математическим развитием) только после рассмотрения ряда примеров, поэтому мы и приводим этот основной принцип не в начале главы (как это было бы естественно для математика), а лишь после решения ряда примеров.
А теперь сформулируем несколько практических рекомендаций, полезных начинающему при постановке задач динамического программирования. Эту постановку удобно проводить в следующем порядке.
1. Выбрать параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом.
2. Расчленить операцию на этапы (шаги).
3. Выяснить набор шаговых управлений х,
для каждого шага и налагаемые на них ограничения.
4. Определить, какой выигрыш приносит на i-м шаге управление хi, если перед этим система была в состоянии S, т. е. записать «функции выигрыша»:
wi
= fi(S,xi). (14.1)
5.
Определить, как изменяется состояние S
системы S под влиянием управления хi на i-м шаге: оно переходит в новое состояние
S ’=

«Функции изменения состояния» (14.2) тоже должны быть записаны1).
6. Записать основное рекуррентное уравнение динамического программирования, выражающее условный оптимальный выигрыш W<(S) (начиная с i-го шага и до конца) через уже известную функцию Wi+1 (S):

Этому выигрышу соответствует условное оптимальное управление на i-м шаге хi(S) (подчеркнем, что в уже известную функцию Wi+1(S) надо вместо S
подставить измененное состояние S ’ =

7. Произвести условную оптимизацию последнего (m-го) шага, задаваясь гаммой состояний S, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждого из них условный оптимальный выигрыш по формуле

и находя условное оптимальное управление xm(S), для которого этот максимум достигается.
8. Произвести условную оптимизацию (m - 1)-го, (m - 2)-го и т. д. шагов по формуле (14.3), полагая в ней i = (m - 1), (m - 2), ..., и для каждого из шагов указать условное оптимальное управление xi(S), при котором максимум* достигается.
Заметим, что если состояние системы в начальный момент известно (а это обычно бывает так), то на первом шаге варьировать состояние системы не нужно — прямо находим оптимальный выигрыш для данного начального состояния So. Это и есть оптимальный выигрыш за всю операцию
W* = Wi(So).
9. Произвести безусловную оптимизацию управления, «читая» соответствующие рекомендации на каждом шаге. Взять найденное оптимальное управление на первом шаге

* * *
Сделаем несколько дополнительных замечаний общего характера. До сих пор мы рассматривали только аддитивные задачи динамического программирования, в которых выигрыш за всю операцию равен сумме выигрышей на отдельных шагах.
Но метод динамического программирования применим также и к задачам с так называемым «мультипликативным» критерием, имеющим вид произведения:

(если только выигрыши ?i положительны). Эти задачи решаются точно так же, как задачи с аддитивным критерием, с той единственной разницей, что в основном уравнении (14.3) вместо знака «плюс» ставится знак умножения X:

В заключение — несколько слов о так называемых «бесконечно шаговых» задачах динамического программирования. На практике встречаются случаи, когда планировать операцию приходится не на строго определенный, а на неопределенно долгий промежуток времени, и нас может интересовать решение задачи оптимального управления безотносительно 'к тому, на каком именно шаге операция заканчивается. В таких случаях бывает удобно рассмотреть в качестве модели явления бесконечно шаговый управляемый процесс, где не существует «особенного» по сравнению с другими последнего шага (все шаги равноправны). Для этого, разумеется, нужно, чтобы функции fi выигрыша и функции ?i изменения состояния не зависели от номера шага. Интересующегося этим случаем читателя отошлем к руководству [10]. Вообще, для более подробного ознакомления с методом динамического программирования полезно обратиться к руководствам [6, 10, 11, 71].
ГЛАВА 5 МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
§ 15. Понятие о марковском процессе
До сих пор мы рассматривали главным образом детерминированные задачи исследования операций и методы оптимизации решений в этих задачах. Начиная с этой главы, и до конца книги мы будем заниматься задачами исследования операций в условиях неопределенности. В этой главе мы рассмотрим сравнительно благоприятный случай «доброкачественной» или «стохастической» неопределенности (см. § 5 гл. 2), когда неопределенные факторы, входящие в задачу, представляют собой случайные величины (или случайные функции), вероятностные характеристики которых либо известны, либо могут быть получены из опыта. Мы будем здесь заниматься, главным образом, прямыми задачами исследования операций, т.
е. построением математических моделей некоторых случайных явлений, лишь бегло останавливаясь на обратных задачах (оптимизации решений), потому что они, как правило, сложны. В стохастических задачах исследования операций часто затруднительно даже построение математической модели, уже не говоря об оптимизации («не до жиру, быть бы живу»). В большинстве случаев не удается построить простую математическую модель, позволяющую в явном (аналитическом) виде найти интересующие нас величины (показатели эффективности) в зависимости от условий операции ? и элементов решения х.
Однако в некоторых особых случаях такую математическую модель удается построить. Это — когда исследуемая операция представляет собой (точно или приближенно) так называемый марковский случайный процесс.
А что такое «марковский случайный процесс»? Определение этого понятия мы дадим не сразу, сначала поговорим о том, что такое вообще «случайный процесс».
Пусть имеется некоторая физическая система S, которая с течением времени меняет свое состояние (переходит из одного состояния в другое), причем заранее неизвестным, случайным образом. Тогда мы будем говорить, что в системе S протекает случайный процесс.
Под «физической системой» можно понимать что угодно: техническое устройство, группу таких устройств, предприятие, отрасль промышленности, живой организм, популяцию и т.д. Большинству процессов, протекающих в реальных системах, свойственны, в той или иной мере, черты случайности, неопределенности.
Пусть, например, система S — космический корабль, выводимый на заданную орбиту. Процесс вывода неизбежно сопровождается случайными ошибками, отклонениями от заданного режима, на которые приходится вводить коррекцию (если бы не случайные ошибки, коррекция была бы не нужна). Значит, процесс вывода на орбиту — случайный процесс.
Теперь спустимся из космоса в околоземную зону. Физическая система S — обыкновенный самолет, совершающий рейс на заданной высоте, по определенному маршруту. Является ли этот процесс случайным? Безусловно, да, так как он неизбежно (в силу турбулентности атмосферы и других факторов) сопровождается случайными возмущениями, колебаниями (в этом не усомнится никто, испытавший на себе так называемую «болтанку» или нарушение графика полетов).
Еще пример: система S — техническое устройство, состоящее из ряда узлов, которые время от времени выходят, из строя, заменяются или восстанавливаются. Процесс, протекающий в этой системе, безусловно, случаен. А столовая самообслуживания? В ней время от времени могут образовываться и рассасываться очереди, возникать задержки, нехватка подносов и т. д.
Вообще, если подумать, труднее привести пример «неслучайного» процесса, чем случайного. Даже процесс хода часов — классический пример точной, строго выверенной работы («работает, как часы») подвержен случайным изменениям (уход вперед, отставание, остановка).
Так что же, выходит, все процессы в природе случайны? Да, строго говоря, это так — случайные возмущения присущи любому процессу. Но до тех пор, пока эти возмущения несущественны, мало влияют на интересующие нас параметры, мы можем ими пренебречь и рассматривать процесс как детерминированный, неслучайный. Необходимость учета случайностей возникает тогда, когда они прямо касаются нашей заинтересованности. Например, составляя расписание самолетов, можно пренебречь случайными колебаниями самолета вокруг центра массы, а проектируя автопилот — безусловно, нет. Большинство процессов, которые мы изучаем в физике, технике, по существу являются случайными, но только некоторые из них мы изучаем как случайные — когда нам это «позарез» надо.
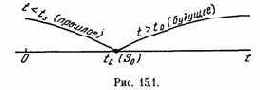
Теперь, когда нам ясно, что такое «случайный процесс», дадим определение «марковского случайного процесса». Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени to вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент to u не зависят от того, когда и как система пришла в это состояние.
Это очень важное определение стоит того, чтобы его растолковать подробнее. Пусть в настоящий момент t0 (см. рис. 15.1) система находится в определенном состоянии So. Мы наблюдаем, процесс со стороны и в момент to знаем состояние системы So и всю предысторию процесса, все, что было при t < to. Нас, естественно, интересует будущее (t > to). Можем ли мы его предугадать (предсказать)? В точности — нет, наш процесс случайный, значит — непредсказуемый.
Но какие-то вероятностные характеристики процесса в будущем мы найти можем. Например, вероятность того, что через некоторое время т система S окажется в состоянии Si или сохранит состояние So, и т. п.
Так вот, для марковского случайного процесса такое «вероятностное предсказание» оказывается гораздо проще, чем для немарковского. Если процесс — марковский, то предсказывать можно, только учитывая настоящее состояние системы So и забыв о его «предыстории» (поведении системы при t < to). Само состояние So, разумеется, зависит от прошлого, но как только оно достигнуто, о прошлом можно забыть. Иначе формулируя, в марковском процессе «будущее зависит от прошлого только через настоящее».
Пример марковского процесса: система S —
счетчик Гейгера, на который время от времени попадают космические частицы; состояние системы в момент t характеризуется показанием счетчика — числом частиц, пришедших до данного момента. Пусть в момент to счетчик показывает So. Вероятность того, что в момент t > to счетчик покажет то или другое число частиц S1 (или не менее S1), разумеется, зависит от S0, но не зависит от того, в какие именно моменты приходили частицы до момента to.
На практике часто встречаются процессы, которые если не в точности марковские, то могут быть в каком-то приближении рассмотрены как марковские. Пример: система S — группа самолетов, участвующих в воздушном бою. Состояние системы характеризуется числом самолетов «красных» — х и «синих» — у, сохранившихся (не сбитых) к какому-то моменту. В момент to нам известны численности сторон — x0 и уо.
Нас интересует вероятность того, что в какой-то момент tо + ?
численный перевес будет на стороне «красных». Спросим себя, от чего зависит эта вероятность? В первую очередь от того, в каком состоянии находится система в данный момент to, а не от того, когда и в какой последовательности погибали сбитые до момента to самолеты.
Итак, более или менее ясно, что такое марковский случайный процесс. Теперь ошеломим читателя неожиданным парадоксом: в сущности, любой процесс можно рассматривать как марковский, если все параметры из «прошлого», от которых зависит «будущее», включить в «настоящее».
Например, пусть речь идет о работе какого-то технического устройства; в какой- то момент to оно еще исправно, и нас интересует вероятность того, что оно проработает еще время т. Если за настоящее состояние системы считать просто «система исправна», то процесс, безусловно, не марковский, потому что вероятность того, что она не откажет за время т, зависит, в общем случае, от того, сколько времени она уже проработала и когда был последний ремонт. Если оба эти параметра (общее время работы и время после последнего ремонта) включить в настоящее состояние системы, то процесс уже можно будет, пожалуй, считать марковским. Однако такое «обогащение настоящего за счет предыстории» далеко не всегда бывает полезно, так как (если число параметров прошлого велико) оно зачастую приводит к «проклятию многомерности», о котором мы уже говорили. Поэтому в дальнейшем, говоря о марковском процессе, мы будем подразумевать его простым, «бесхитростным», с небольшим числом параметров, определяющих «настоящее».
На практике марковские процессы в чистом виде обычно не встречаются, но нередко приходится иметь дело с процессами, для которых влиянием «предыстории» можно пренебречь. При изучении таких процессов можно с успехом применять марковские модели. Мы в дальнейшем увидим, как это делается.
В исследовании операций большое значение имеют так называемые марковские случайные процессы с дискретными состояниями и непрерывным временем. Процесс называется процессом с дискретными состояниями, если его возможные состояния S1, S2, S3,... можно заранее перечислить (перенумеровать), и переход системы из состояния в состояние происходит «скачком», практически мгновенно. Процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние не фиксированы заранее, а неопределенны, случайны, если переход может осуществиться, в принципе, в любой момент. Мы здесь будем рассматривать только процессы с дискретными состояниями и непрерывным временем.
Пример такого процесса: техническое устройство S состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя (отказать), после чего мгновенно начинается ремонт узла, тоже продолжающийся заранее неизвестное, случайное время.
Возможные состояния системы можно перечислить:
So — оба узла исправны,
S1 — первый узел ремонтируется, второй исправен,
S2 — второй узел ремонтируется, первый исправен,
S3 — оба узла ремонтируются.
Переходы системы S из состояния в состояние происходят практически мгновенно, в случайные моменты выхода из строя того или другого узла или окончания ремонта.
При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой — так называемым графом состояний. Состояния системы изображаются прямоугольниками (или кругами, или даже точками), а возможные переходы из состояния в состояние — стрелками, соединяющими состояния. Мы будем изображать состояния прямоугольниками, в которых записаны обозначения состояний: S1, S2, ... Sn.
Построим граф состояний для рассмотренного выше примера (см. рис. 15.2). Стрелка, направленная из So в S1, означает переход в момент отказа первого узла; стрелка, направленная обратно, из S1 в So,— переход в момент окончания ремонта этого узла. Остальные стрелки объясняются аналогично.
Внимательный читатель может спросить: а почему нет стрелки, ведущей непосредственно из So в S3? Разве не может быть, что оба узла откажут одновременно, например, вследствие короткого замыкания? Вопрос законный. Ответим, что мы предполагаем узлы выходящими из строя независимо друг от друга, а вероятностью строго одновременного выхода их из строя пренебрегаем (ниже будет дано более точно обоснование этого допущения).
Если процесс, протекающий в системе с дискретными состояниями и непрерывным временем, является марковским, то для его описания можно построить довольно простую математическую модель. Но перед тем, как ее строить, нам полезно познакомиться с важным понятием теории вероятностей — понятием «потока событий».
§ 16. Потоки событий
Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени. Например: поток вызовов на телефонной станции; поток отказов (сбоев) ЭВМ; поток железнодорожных составов, поступающих на сортировочную станцию; поток частиц, попадающих на счетчик Гейгера, и т.
д.
Поток событий можно наглядно изобразить рядом точек на оси времени Ot (рис. 16.1); не надо только забывать, что положение каждой из них случайно, и на рис. 16.1 изображена только какая-то одна реализация
потока.

рис. 16.1.
Говоря о «потоке событий», нужно иметь в виду, что здесь термин «событие» имеет значение, несколько отличное от того, к которому мы привыкли в теории вероятностей. Там «событием» (или «случайным событием») называется какой-то исход опыта, обладающий той или другой вероятностью. События, образующие поток, сами по себе вероятностями не обладают;
вероятностями обладают другие, производные от них события, например: «на участок времени ? (рис. 16.1) попадет ровно два события», или «на участок времени ?t попадет хотя бы одно событие», или «промежуток времени между двумя соседними событиями будет не меньше t».
Важной характеристикой потока событий является его интенсивность ? — среднее число событий, приходящееся на единицу времени. Интенсивность потока может быть как постоянной (? = const.), так и переменной, зависящей от времени t. Например, поток автомашин, движущихся по улице, днем интенсивнее, чем ночью, в часы пик — интенсивнее, чем в другие часы.
Поток событий называется регулярным, если события следуют одно за другим через определенные, равные промежутки времени. На практике чаще встречаются потоки не регулярные, со случайными интервалами.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность \
стационарного потока должна быть постоянной. Это отнюдь не значит, что фактическое число событий, появляющееся в единицу времени, постоянно,— нет, поток неизбежно (если только он не регулярный) имеет какие-то случайные сгущения и разрежения, как, например, показано на рис. 16.1. Важно, что для стационарного потока эти сгущения и разрежения не носят закономерного характера: на один участок длины 1 может попасть больше, а на другой — меньше событий, но среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.
Одна из типичных ошибок начинающих — это принимать случайные сгущения и разрежения потока за изменения его интенсивности. Предостережем читателя от этой ошибки!
Как правило, отклонения от стационарности могут быть объяснены какими-то физическими причинами. Например, совершенно естественно, интенсивность потока вызовов, поступающих на АТС, ночью меньше, чем днем (ночью люди имеют обыкновение спать). Увеличение интенсивности потока покупателей, приходящих в магазин, в часы после окончания рабочего дня тоже имеет физическое объяснение. Если поток событий имеет тенденцию к явно выраженным сгущениям и разрежением (особенно периодическим), нужно всегда заподозрить физическую причину и постараться ее выявить.
На практике часто встречаются потоки событий, которые (по крайней мере, на ограниченном участке времени) могут считаться стационарными. Например, поток вызовов, поступающих на АТС между 13 и 14 часами, практически стационарен; тот же поток в течение суток уже не стационарен1).
Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени



(хотя бы потому, что интервал по времени между отдельными покупателями не может быть меньше, чем минимальное время to обслуживания каждого из них). Так же обстоит дело и с потоком поездов, подходящих к станции (между ними всегда существует какой-то минимальный интервал to, выбираемый из соображений безопасности). Впрочем, если минимальный интервал между событиями много меньше среднего интервала между ними t = 1А, иногда наличием последействия можно пренебречь.
Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу. Например, поток клиентов, направляющихся в парикмахерскую или к зубному врачу, обычно ординарен, чего нельзя сказать о потоке клиентов, направляющихся в загс для регистрации брака. Поток поездов, подходящих к станции, ординарен, а поток вагонов — неординарен. Если поток событий ординарен, то вероятностью попадания на малый участок времени At двух или более событий можно пренебречь.
Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и не имеет последействия. Название «простейший» связано с тем, что процессы, связанные с простейшими потоками, имеют наиболее простое математическое описание. Между прочим, самый простой, на первый взгляд, регулярный поток не является «простейшим», так как обладает последействием: моменты появления событий в таком потоке связаны жесткой, функциональной зависимостью. Без специальных усилий по поддержанию его регулярности такой поток обычно не создается.
Простейший поток играет среди других потоков особую роль, в чем-то подобную роли нормального закона среди других законов распределения. А именно, при наложении (суперпозиции) достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.
Легко доказать (см., например, [l2] или любой учеб-пик по теории вероятностей),что для простейшего потока с интенсивностью

между соседними событиями имеет так называемое показательное распределение с плотностью
f(t) =

(см. рис. 16.3). Величина

есть величина, обратная параметру, а среднее квадратическое отклонение


В теории вероятностей в качестве « меры случайности» неотрицательной случайной величины нередко рассматривают так называемый коэффициент вариации:

Из формул (16.2), (16.3) следует, что для показательного распределения vТ = 1, т. е. для простейшего потока событий коэффициент вариации интервалов между событиями равен единице.
Очевидно, что для регулярного потока событий, у которого интервал между событиями вообще не случаен (

В расчетах, связанных с потоками событий, очень удобно пользоваться понятием «элемента вероятности». Рассмотрим на оси Ot простейший поток с интенсивностью




т. е. для простейшего потока элемент вероятности равен интенсивности потока, умноженной на длину элементарного участка. Заметим, что элемент вероятности, в силу отсутствия последействия, совершенно не зависит 'от того, сколько событий и когда появлялись ранее.
Заметим также, что с точностью до величин высшего порядка малости вероятность появления хотя бы одного события на элементарном участке At равна вероятности появления ровно одного события па этом участке. Это вытекает из ординарности простейшего потока2).
Поток событий называется рекуррентным (иначе—«потоком Пальма»), если он стационарен, ординарен, а интервалы времени между событиями Т1, Т2, Т3, ... (см.
рис. 16.4) представляют собой независимые случайные величины с одинаковым произвольным распределением (например, с плотностью, показанной на рис. 16.5).
1) Можно придумать искусственные примеры потоков, для которых vТ > 1, но природа таких фокусов обычно не устраивает.
2) Вспомним, как мы не проставили стрелок из состояния S0 в S3 и обратно на рис. 15.2. Это объясняется тем, что как потоки отказов. так и потоки восстановлении узлов мы считали ординарными.
Приведем пример рекуррентного потока. Технический элемент (скажем, радиолампа) работает непрерывно до своего отказа (выхода из строя); отказавший элемент мгновенно заменяется новым. Если отдельные экземпляры элемента выходят из строя независимо друг от друга, то поток отказов (он же
О t Рис. 16.4.
«поток замен» или «восстановлении») будет рекуррентным.
Другой пример. Продавец в магазине непрерывно занят обслуживанием покупателей (как это бывает в часы максимальной нагрузки). Обслуживание покупателя продолжается случайное время Т. Тогда поток обслуженных покупателей будет рекуррентным (если считать, что времена обслуживания отдельных покупателей независимы и, например, ссора между продавцом и покупателем не скажется на времени обслуживания других).
Очевидно, простейший поток представляет собой частный случай рекуррентного потока, когда интервалы между событиями имеют показательное распределение (16.1). Другим частным (вырожденным) случаем рекуррентного потока является регулярный поток событий, где интервалы вообще не случайны, постоянны.
Целую гамму рекуррентных потоков событий, обладающих разной степенью упорядоченности, можно получить «просеиванием» простейшего потока. Пусть, например, в какое-то учреждение поступает простейший поток посетителей, а у входа стоит «страж», направляющий первого посетителя — к первому столу, второго — ко второму столу и т. д. Если столов n, то на каждый из них поступает так называемый «поток Эрланга п-го порядка».
Такой поток получается из простейшего, если сохранять в потоке каждое n-е событие, а промежуточные — выбрасывать. Простейший поток есть не что иное, как поток Эрланга первого порядка. Можно показать, что при таком просеивании простейшего потока коэффициент вариации интервалов уменьшается, и при увеличении порядка п поток Эрланга приближается к регулярному. Коэффициент вариации интервалов между событиями потока Эрланга n-го порядка равен

§ 17. Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний
Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, нам удобно будет представлять себе, что все переходы системы S из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, поток отказов, поток восстановлении и т. д.). Если все потоки событий, переводящие систему S из состояния в состояние,— простейшие, то процесс протекающий в системе, будет марковским1). Это и естественно, так как простейший ноток не обладает последействием: в нем «будущее» не зависит от «прошлого».
Если система S находится в каком-то состоянии Si, из которого есть непосредственный переход в другое состояние Sj (стрелка, ведущая из Si, в Sj на графе состояний), то мы себе это будем представлять так, как будто па систему, пока она находится в состоянии Si действует простейший поток событий, переводящий её по стрелке Si

Для наглядности очень удобно на графе состояний у каждой стрелки проставлять интенсивность того потока событий, который переводит систему по данной стрелке. Обозначим

1) Простейший характер потоков — достаточное, но не необходимое условие для того, чтобы процесс был марковским.
Построим размеченный граф состояний для примера, данного в § 15 (техническое устройство из двух узлов). Напомним состояния системы:
S0 — оба узла исправны,
S1 — первый узел ремонтируется, второй исправен,
S2 — второй узел ремонтируется, первый исправен,
S3 — оба узла ремонтируются.
Интенсивности потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта узла не зависит
 |
 |


Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.
В самом деле, пусть рассматривается система S, имеющая п возможных состояний S1, S2, ..., Sn. Назовем вероятностью i-го состояния вероятность pi(t) того, что в момент t система будет находиться в состоянии Si. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
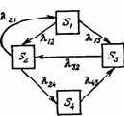 |
Покажем на конкретном примере, как эти уравнения составляются. Пусть система S имеет четыре состояния: S1, S2, S3, S4, размеченный граф которых показан на рис. 17.3. Рассмотрим одну из вероятностей состояний, например pi(t). Это—вероятность того, что в момент t система будет в состоянии S1. Придадим t малое приращение





Найдем вероятность первого варианта. Вероятность того, что в момент t
система была в состоянии S1, равна p1(t). Эту вероятность нужно умножить на вероятность того, что, находившись в момент t в состоянии S1, система за время







Найдем вероятность второго варианта. Она равна вероятности того, что в момент t система будет в состоянии S2, а за время


Складывая вероятности обоих вариантов (по правилу сложения вероятностей), получим:

Раскроем квадратные скобки, перенесем pi(t) в левую часть и разделим обе части на


Устремим, как и полагается в подобных случаях,


или, короче, отбрасывая аргумент t у функций p1, p2 (теперь он нам больше уже не нужен):

Рассуждая аналогично для всех остальных состояний, напишем еще три дифференциальных уравнения. Присоединяя к ним уравнение (17.2), получим систему дифференциальных уравнений для вероятностей состояний:
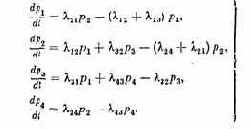
Это — система четырех линейных дифференциальных уравнений с четырьмя неизвестными функциями p1, р2, р3, р4. Заметим, что одно из них (любое) можно отбросить, пользуясь тем, что p1 + p2 + р3 + р4 = 1: выразить любую из вероятностей pi через другие, это выражение подставить в (17.3), а соответствующее уравнение с производной

Сформулируем теперь общее правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности какого-то (i-го) состояния. В правой части — сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го) состояния.
Пользуясь этим правилом, запишем уравнения Колмогорова для системы S, размеченный граф состояний которой дан на рис. 17.2:
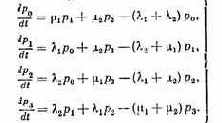
Чтобы решить уравнения Колмогорова и найти вероятности состояний, прежде всего надо задать начальные условия. Если мы точно знаем начальное состояние системы Si, то в начальный момент (при t = 0) pi(0) = 1, а все остальные начальные вероятности равны пулю. Так, например, уравнения (17.4) естественно решать при начальных условиях p0(0) = 1,p1(0) = p2(0) = p3(0) = 0 (в начальный момент оба узла исправны).
Как решать подобные уравнения? Вообще говоря, линейные дифференциальные уравнения с постоянными коэффициентами можно решать аналитически, но это удобно только когда число уравнений не превосходит двух (иногда — трех). Если уравнений больше, обычно их решают численно — вручную или на ЭВМ.
Таким образом, уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени.
Поставим теперь вопрос: что будет происходить с вероятностями состояний при t

Предположим, что это условие выполнено и финальные вероятности существуют:

Финальные вероятности мы будем обозначать теми же буквами р1, р2, ..., что и сами вероятности состояний, но разумея под ними уже не переменные величины (функции времени), а постоянные числа. Очевидно, они тоже образуют в сумме единицу:
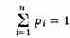
Как понимать эти финальные вероятности? При t

устанавливается предельный стационарный режим, в ходе которого система случайным образом меняет свои состояния, но их вероятности уже не зависят от времени. Финальную вероятность состояния S,
можно истолковать как среднее относительное время пребывания системы в этом состоянии. Например, если система S
имеет три состояния S1, S2, S3 и их финальные вероятности равны 0,2, 0,3 и 0,5, это значит, что в предельном, стационарном режиме система в среднем две десятых времени проводит в состоянии S1, три десятых — в состоянии S2 и половину времени — в состоянии S3.
1) Это условие достаточно, но не необходимо для существования финальных вероятностей.
Как же вычислить финальные вероятности? Очень просто. Если вероятности pi, pa,. •. постоянны, то их производные равны нулю. Значит, чтобы найти финальные вероятности, нужно все левые части в уравнениях Колмогорова положить равными нулю и решить полученную систему уже не дифференциальных, а линейных алгебраических уравнений. Можно и не писать уравнений Колмогорова, а прямо по графу состояний написать систему линейных алгебраических уравнений.
Если перенести отрицательный член каждого уравнения из правой части в левую, то получим сразу систему уравнений, где слева стоит финальная вероятность данного состояния pi, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-e состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пользуясь этим правилом, напишем линейные алгебраические уравнения для финальных вероятностей состояний системы, граф состояний которой дан на рис. 17.2:
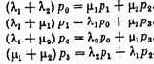
Эту систему четырех уравнений с четырьмя неизвестными р0, р1, р2, р3, казалось бы, вполне можно решить. Но вот беда: уравнения (17.7) однородны (не имеют свободного члена) и, значит, определяют неизвестные только с точностью до произвольного множителя. К счастью, мы можем воспользоваться так называемым нормировочным условием:
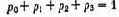
и с его помощью решить систему. При этом одно (любое) из уравнений можно отбросить (оно вытекает как следствие из остальных).
Давайте зададимся численными значениями интенсивностей




вместо него нормировочное условие (17.8).Уравнения примут вид:

Решая их, получим:
p0 = 6/15 = 0,40; p1 = 3/15 = 0,20; p2 = 4/15 ? 0,27;
p3 = 2/15 ? 0,13,
т. е. в предельном, стационарном режиме система S в среднем 40% времени будет проводить в состоянии So (оба узла исправны), 20% —в состоянии S1 (первый узел ремонтируется, второй работает), 27% —в состоянии S2
(второй узел ремонтируется, первый работает) и 13% —в состоянии S3 полной негодности (оба узла ремонтируются). Знание этих финальных вероятностей может помочь оценить среднюю эффективность работы системы и загрузку ремонтных органов. Предположим, что система S в состоянии S0 (полностью исправная) приносит в единицу времени доход 8 (условных единиц), в состоянии S1 – доход 3, в состоянии S2 – доход 5, в состоянии S3 — вообще не приносит дохода.
Тогда в предельном, стационарном режиме средний доход в единицу времени будет
W = 0,40 · 8 +0,20 · 3 + 0,27 · 5 = 5,15.
Теперь оценим загрузку ремонтных органов (рабочих), занятых ремонтом узлов 1 и 2. Узел 1 ремонтируется долю времени, равную р1 + р3 = 0,20+0,13 = 0,33. Узел 2 ремонтируется долю времени р2
+ р3 = 0,40.
Здесь уже может возникнуть вопрос об оптимизации решения. Допустим, что мы можем уменьшить среднее время ремонта того или другого узла (может быть, в того, и другого), но это нам обойдется в какую-то сумму. Спрашивается, «стоит ли овчинка выделки»? Т. е. окупит ли увеличение дохода, связанное с ускорением ремонта, повышенные расходы на ремонт?
Предоставим читателю самостоятельно поставить и решить такую экономическую задачу. При этом ему придется решать систему четырех уравнений с четырьмя неизвестными, но это ничего (характер, как известно, укрепляется в бедствиях!),
ГЛАВА 6
ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
§ 18. Задачи теории массового обслуживания. Классификация систем массового обслуживания
При исследовании операций часто приходится сталкиваться с работой своеобразных систем, называемых системами массового обслуживания (СМО). Примерами таких систем могут служить: телефонные станции, ремонтные мастерские, билетные кассы, справочные бюро, магазины, парикмахерские и т. п.
Каждая СМО состоит из какого-то числа обслуживающих единиц (или «приборов»), которые мы будем называть каналами обслуживания. Каналами могут быть: линии связи, рабочие точки, кассиры, продавцы, лифты, автомашины и др. СМО могут быть одноканальными и многоканальными.
Всякая СМО предназначена для обслуживания какого-то потока заявок (или «требований»), поступающих в какие-то случайные моменты времени. Обслуживание заявки продолжается какое-то, вообще говоря, случайное время Тоб, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времен обслуживания приводит к тому, что в какие-то периоды времени на входе СМО скапливается излишне большое число заявок (они либо становятся в очередь, либо покидают СМО не обслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать.
Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем; состояние СМО меняется скачком в моменты появления каких-то событий (или прихода новой заявки, или окончания обслуживания, или момента, когда заявка, которой надоело ждать, покидает очередь).
Предмет теории массового обслуживания — построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками — показателями эффективности СМО, описывающими, с той или другой точки зрения, ее способность справляться с потоком заявок. В качестве таких показателей (в зависимости от обстановки и целей исследования) могут применяться разные величины, например: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди и среднее время ожидания обслуживания; вероятность того, что число заявок в очереди превысит какое-то значение, и т. д. Среди заданных условий работы СМО мы намеренно не выделяем элементов решения: ими могут быть, например, число каналов, их производительность, режим работы СМО и т. д. Важно уметь решать прямые задачи исследования операций, а обратные ставятся и решаются в зависимости от того, какие именно параметры нам нужно выбирать или изменять. Что касается задач оптимизации, то мы ими здесь почти не будем заниматься, разве только в простейших случаях.
Математический анализ работы СМО очень облегчается, если процесс этой работы — марковский. Мы уже знаем, что для этого достаточно, чтобы все потоки событий, переводящие систему из состояния в состояние (потоки заявок, потоки «обслуживании»), были простейшими. Если это свойство нарушается, то математическое описание процесса становится гораздо сложнее и довести его до явных, аналитических формул удается лишь в редких случаях. Однако все же аппарат простейшей, марковской теории массового обслуживания может пригодиться для приближенного описания работы СМО даже в тех случаях, когда потоки событий — не простейшие.
Во многих случаях для принятия разумного решения по организации работы СМО вовсе и не требуется точного знания всех ее характеристик — зачастую достаточно и приближенного, ориентировочного.
Системы массового обслуживания делятся на типы (или классы) по ряду признаков. Первое деление: СМО с отказами и СМО с очередью. В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует.,» Примеры СМО с отказами встречаются в телефонии: заявка на разговор, пришедшая в момент, когда все каналы связи заняты, получает отказ и покидает СМО не обслуженной. В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной. На практике чаще встречаются (и имеют большее значение) СМО с очередью; недаром теория массового обслуживания имеет второе название: «теория очередей».
СМО с очередью подразделяются на разные виды, в зависимости от того, как организована очередь — ограничена она или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания (так называемые «СМО с нетерпеливыми заявками»). При анализе СМО должна учитываться также и «дисциплина обслуживания» — заявки могут обслуживаться либо в порядке поступления (раньше пришла, раньше обслуживается), либо в случайном порядке. Нередко встречается так называемое обслуживание с приоритетом — некоторые заявки обслуживаются вне очереди. Приоритет может быть как абсолютным — когда заявка с более высоким приоритетом «вытесняет» из-под обслуживания заявку с низшим (например, пришедший в парикмахерскую клиент высокого ранга прогоняет с кресла обыкновенного клиента), так и относительным—когда начатое обслуживание доводится до конца, а заявка с более высоким приоритетом имеет лишь право на лучшее место в очереди.
Существуют СМО с так называемым многофазовым обслуживанием, состоящим из нескольких последовательных этапов или «фаз» (например, Покупатель, пришедший в магазин, должен сначала выбрать товар, затем оплатить его в кассе, затем получить на контроле).
Кроме этих признаков, СМО делятся на два класса:
«открытые» и «замкнутые». В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии - сама СМО (сколько каналов занято). В замкнутой СМО—зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока «требований» со стороны станков зависит от того, сколько их уже неисправно и ждет наладки. Это — пример замкнутой СМО. Классификация СМО далеко не ограничивается приведенными их разновидностями, но мы ограничимся ими.
Оптимизация работы СМО может производиться под разными углами зрения: с точки зрения организаторов (или владельцев) СМО или с точки зрения обслуживаемых клиентов. С первой точки зрения желательно «выжать все, что возможно» из СМО и добиться того, чтобы ее каналы были предельно загружены. С точки зрения клиентов желательно всемерное уменьшение очередей, которые зачастую становятся настоящим «бичом быта», приводя к бессмысленной трате сил и времени и, в конечном итоге, к понижению производительности труда. При решении задач оптимизации в теории массового обслуживания существенно необходим «системный подход», полное и комплексное рассмотрение всех последствий каждого решения. Например, с точки зрения клиентов СМО желательно увеличение числа каналов обслуживания; но ведь работу каждого канала надо оплачивать, что удорожает обслуживание. Построение математической модели позволяет решить оптимизационную задачу о разумном числе каналов с учетом всех «за» и «против». Поэтому мы не выделяем в задачах массового обслуживания какого-либо одного показателя эффективности, а сразу ставим эти задачи как многокритериальные.
Все перечисленные выше разновидности СМО (и многие другие, здесь не упомянутые) исследуются в теории массового обслуживания, литература по которой в настоящее время достигла огромных размеров. Мы назовем только несколько книг: [13—17]. Кроме того, разделы, посвященные теории массового обслуживания, имеются в ряде книг по исследованию операций: [1, 6, 7].
Однако почти нигде изложение не ведется на должном методическом уровне: выводы часто проводятся излишне сложно; верные (почти всегда) формулы доказываются не лучшим путем1). В настоящем (по необходимости кратком) изложении теории массового обслуживания мы приведем два методических приема, позволяющих сильно упростить выводы формул. Этим приемам будет посвящен следующий параграф.
1) К сожалению, этим недостатком страдает и книга [6] автора, где ряд выводов получен недостаточно просто.
§ 19. Схема гибели и размножения. Формула Литтла
1.Схема гибели и размножения. Мы знаем, что, имея в распоряжении размеченный граф состояний, можно легко написать уравнения Колмогорова для вероятностей состояний, а также написать и решить алгебраические уравнения для финальных вероятностей. Для некоторых случаев удается последние уравнения

Рис.19.1
решить заранее, в буквенном виде. В частности, это удается сделать, если граф состояний системы представляет собой так называемую «схему гибели и размножения».
Граф состояний для схемы гибели и размножения имеет вид, показанный на рис. 19.1. Особенность этого графа в том, что все состояния системы можно вытянуть в одну цепочку, в которой каждое из средних состояний (S1, S2,…,Sn-1) связано прямой и обратной стрелкой с каждым из соседних состояний — правым и левым, а крайние состояния (S0, Sn) — только с одним соседним состоянием. Термин «схема гибели и размножения» ведет начало от биологических задач, где подобной схемой описывается изменение численности популяции.
Схема гибели и размножения очень часто встречается в разных задачах практики, в частности — в теории массового обслуживания, поэтому полезно, один раз и навсегда, найти для нее финальные вероятности состояний.
Предположим, что все потоки событии, переводящие систему по стрелкам графа,— простейшие (для краткости будем называть и систему S и протекающий в ней процесс — простейшими).
Пользуясь графом рис. 19.1, составим и решим алгебраические уравнения для финальных вероятностей состоянии), существование вытекает из того, что из каждого состояния можно перейти в каждое другое, в число состояний конечно).
Для первого состояния S0 имеем:

Для второго состояния S1:

В силу (19.1) последнее равенство приводится к виду

далее, совершенно аналогично

и вообще

где k принимает все значения от 0 до п. Итак, финальные вероятности p0, p1,..., рn удовлетворяют уравнениям

кроме того, надо учесть нормировочное условие
p0 + p1 + p2
+…+ pn =1. (19.3)
Решим эту систему уравнений. Из первого уравнения (19.2) выразим p1 через р0:
p1 =

Из второго, с учетом (19.4), получим:

• из третьего, с учетом (19.5),

и вообще, для любого k (от 1 до n):

Обратим внимание на формулу (19.7). В числителе стоит произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо (с начала и до данного состояния Sk), а в знаменателе — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево (с начала и до Sk).
Таким образом, все вероятности состояний р0, p1, ..., рn выражены через одну из них (р0). Подставим эти выражения в нормировочное условие (19.3). Получим, вынося за скобку р0:

отсюда получим выражение для р0:

(19.8)
(скобку мы возвели в степень -1, чтобы не писать двухэтажных дробей). Все остальные вероятности выражены через р0 (см. формулы (19.4) — (19.7)). Заметим, что коэффициенты при р0 в каждой из них представляют собой не что иное, как последовательные члены ряда, стоящего после единицы в формуле (19.8). Значит, вычисляя р0, мы уже нашли все эти коэффициенты.
Полученные формулы очень полезны при решении простейших задач теории массового обслуживания.
2. Формула Литтла.
Теперь мы выведем одну важную формулу, связывающую (для предельного, стационарного режима) среднее число заявок Lсист, находящихся в системе массового обслуживания (т.
е. обслуживаемых или стоящих в очереди), и среднее время пребывания заявки в системе Wсист.
Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной или с ограниченной очередью) и связанные с нею два потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют одну и ту же интенсивность ?.
Обозначим: X(t} — число заявок, прибывших в СМО до момента t. Y(t) —
число заявок покинувших СМО
до момента t. И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов заявок (X(t)) и уходов заявок (Y(t)). Вид функций X(t) и Y(t) показан на рис. 19.2; обе линии — ступенчатые, верхняя — X(t), нижняя—Y(t). Очевидно, что для любого момента t их разность Z(t) = X(t) — Y(t) есть не что иное, как число заявок, находящихся в СМО. Когда линии X(t) и Y(t) сливаются, в системе нет заявок.
Рассмотрим очень большой промежуток времени Т (мысленно продолжив график далеко за пределы чертежа) и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции Z(t) на этом промежутке, деленному на длину интервала Т:
Lсист. =

Но этот интеграл представляет собой не что иное, как площадь фигуры, заштрихованной на рис. 19.2. Разглядим хорошенько этот рисунок. Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т. д.). Обозначим эти времена t1, t2,... Правда, под конец промежутка Т некоторые прямоугольники войдут в заштрихованную фигуру не полностью, а частично, но при достаточно большом Т эти мелочи не будут играть роли. Таким образом, можно считать, что

где сумма распространяется на все заявки, пришедшие за время Т.
Разделим правую и левую часть (.19.10) на длину интервала Т. Получим, с учетом (19.9),
Lсист. =

Разделим и умножим правую часть (19.11) на интенсивность X:
Lсист. =

Но величина Т? есть не что иное, как среднее число заявок, пришедших за время Т. Если мы разделим сумму всех времен ti на среднее число заявок, то получим среднее время пребывания заявки в системе Wсист. Итак,
Lсист. = ?Wсист.,
Откуда
Wсист. =

Это и есть замечательная формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.
Точно таким же образом выводится вторая формула Литтла, связывающая среднее время пребывания заявки в очереди Wоч и среднее число заявок в очереди Lоч:
Wоч =

Для вывода достаточно вместо нижней линии на рис. 19.2 взять функцию U(t) — количество заявок, ушедших до момента t не из системы, а из очереди (если заявка, пришедшая в систему, не становится в очередь, а сразу идет под обслуживание, можно все же считать, что она становится в очередь, но находится в ней нулевое время).
Формулы Литтла (19.12) и (19.13) играют большую роль в теории массового обслуживания. К сожалению, в большинстве существующих руководств эти формулы (доказанные в общем виде сравнительно недавно) не приводятся1).
§ 20. Простейшие системы массового обслуживания и их характеристики
В этом параграфе мы рассмотрим, некоторые простейшие СМО и выведем выражения для их характеристик (показателей эффективности). При этом мы продемонстрируем основные методические приемы, характерные для элементарной, «марковской» теории массового обслуживания. Мы не будем гнаться за количеством образцов СМО, для которых будут выведены конечные выражения характеристик; данная книга — не справочник по теории массового обслуживания (такую роль гораздо лучше выполняют специальные руководства).
Наша цель — познакомить читателя с некоторыми «маленькими хитростями», облегчающими путь сквозь теорию массового обслуживания, которая в ряде имеющихся (даже претендующих на популярность) книг может показаться бессвязным набором примеров.
Все потоки событий, переводящие СМО из состояния в состояние, в данном параграфе мы будем считать простейшими (не оговаривая это каждый раз специально). В их числе будет и так называемый «поток обслуживании». Под ним разумеется поток заявок, обслуживаемых одним непрерывно занятым каналом. В этом потоке интервал между событиями, как и всегда в простейшем потоке, имеет показательное распределение (во многих руководствах вместо этого говорят: «время обслуживания — показательное», мы и сами в дальнейшем будем пользоваться таким термином).
1) В популярной книжке [18] дан несколько иной, по сравнению с вышеизложенным, вывод формулы Литтла. Вообще, знакомство с этой книжкой («Беседа вторая») полезно для первоначального ознакомления с теорией массового обслуживания.
В данном параграфе показательное распределение времени обслуживания будет само собой разуметься, как всегда для «простейшей» системы.
Характеристики эффективности рассматриваемых СМО мы будем вводить по ходу изложения.
1. п -канальная СМО с отказами (задача Эрланга). Здесь мы рассмотрим одну из первых по времени, «классических» задач теории массового обслуживания;
эта задача возникла из практических нужд телефонии и была решена в начале нашего века датским математиком Эрлантом. Задача ставится так: имеется п каналов (линий связи), на которые поступает поток заявок с интенсивностью ?. Поток обслуживании имеет интенсивность ? (величина, обратная среднему времени обслуживания tоб). Найти финальные вероятности состояний СМО, а также характеристики ее эффективности:
А — абсолютную пропускную способность, т. е. среднее число заявок, обслуживаемых в единицу времени;
Q — относительную пропускную способность, т. е. среднюю долю пришедших заявок, обслуживаемых системой;
Ротк — вероятность отказа, т. е. того, что заявка покинет СМО не обслуженной;
k — среднее число занятых каналов.
Решение. Состояния системы S
(СМО) будем нумеровать по числу заявок, находящихся в системе (в данном случае оно совпадает с числом занятых каналов):
S0 — в СМО нет ни одной заявки,
S1 — в СМО находится одна заявка (один канал занят, остальные свободны),
Sk — в СМО находится k
заявок (k каналов заняты, остальные свободны),
Sn — в СМО находится п заявок (все n каналов заняты).
Граф состояний СМО соответствует схеме гибели в размножения (рис. 20.1). Разметим этот граф — проставим у стрелок интенсивности потоков событий. Из S0 в S1 систему переводит поток заявок с интенсивностью ? (как только приходит заявка, система перескакивает из S0
в S1). Тот же поток заявок переводит

систему из любого левого состояния в соседнее правое (см. верхние стрелки на рис. 20.1).
Проставим интенсивности у нижних стрелок. Пусть система находится в состоянии S1 (работает один канал). Он производит ? обслуживании в единицу времени. Проставляем у стрелки S1 > S0 интенсивность ?. Теперь представим себе, что система находится в состоянии S2 (работают два канала). Чтобы ей перейти в S1, нужно, чтобы либо закончил обслуживание первый канал, либо второй; суммарная интенсивность их потоков обслуживании равна 2?; проставляем ее у соответствующей стрелки. Суммарный поток обслуживании, даваемый тремя каналами, имеет интенсивность 3?, k каналами — k?. Проставляем эти интенсивности у нижних стрелок на рис. 20.1.
А теперь, зная все интенсивности, воспользуемся уже готовыми формулами (19.7), (19.8) для финальных вероятностей в схеме гибели и размножения. По формуле (19.8) получим:

Члены разложения

в выражениях для p1
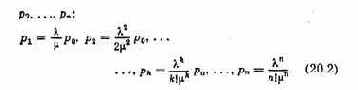
Заметим, что в формулы (20.1), (20.2) интенсивности ? и ? входят не по отдельности, а только в виде отношения ?/?. Обозначим
?/? = ? (20.3)
и будем называть величину р «приведенной интенсивностью потока заявок». Ее смысл— среднее число заявок, приходящее за среднее время обслуживания одной заявки. Пользуясь этим обозначением, перепишем формулы (20.1), (20.2) в виде:


Формулы (20.4), (20.5) для финальных вероятностей состояний называются формулами Эрланга — в честь основателя теории массового обслуживания. Большинство других формул этой теории (сегодня их больше, чем грибов в лесу) не носит никаких специальных имен.
Таким образом, финальные вероятности найдены. По ним мы вычислим характеристики эффективности СМО. Сначала найдем Ротк.
— вероятность того, что пришедшая заявка получит отказ (не будет обслужена). Для этого нужно, чтобы все п
каналов были заняты, значит,
Ротк = рn =

Отсюда находим относительную пропускную способность — вероятность того, что заявка будет обслужена:
Q = 1 – Pотк. = 1 -

Абсолютную пропускную способность получим, умножая интенсивность потока заявок ?, на Q:
A = ?Q = ?

Осталось только найти среднее число занятых каналов k. Эту величину можно было бы найти «впрямую», как математическое ожидание дискретной случайной величины с возможными значениями 0, 1, ..., п
и вероятностями этих значений р0
р1, ..., рn:
k = 0 · р0
+ 1 · p1 + 2 · р2
+ ... + п · рn.
Подставляя сюда выражения (20.5) для рk, (k = 0, 1, ..., п) и выполняя соответствующие преобразования, мы, в конце концов, получили бы верную формулу для k. Но мы выведем ее гораздо проще (вот она, одна из «маленьких хитростей»!) В самом деле, нам известна абсолютная пропускная способность А.
Это — не что иное, как интенсивность потока обслуженных системой заявок. Каждый занятый i .шал в единицу времени обслуживает в среднем |л заявок. Значит, среднее число занятых каналов равно
k = A/?, (20.9)
или, учитывая (20.8),
k =

Рекомендуем читателю самостоятельно решить пример. Имеется станция связи с тремя каналами (n = 3), интенсивность потока заявок ? = 1,5 (заявки в минуту); среднее время обслуживания одной заявки tоб = 2 (мин.), все потоки событий (как и во всем этом параграфе) — простейшие. Найти финальные вероятности состояний и характеристики эффективности СМО: А, Q, Pотк, k. На всякий случай сообщаем ответы: p0 = 1/13, p1 = 3/13, p2 = 9/26, р3
= 9/26 ? 0,346,
А ? 0,981, Q ? 0,654, Pотк ? 0,346, k ? 1,96.
Из ответов видно, между прочим, что наша СМО в значительной мере перегружена: из трех каналов занято в среднем около двух, а из поступающих заявок около 35% остаются не обслуженными. Предлагаем читателю, если он любопытен и неленив, выяснить: сколько потребуется каналов для того, чтобы удовлетворить не менее 80% поступающих заявок? И какая доля каналов при этом будет простаивать?
Тут уже проглядывает некоторый намек на оптимизацию. В самом деле, содержание каждого канала в единицу времени обходится в какую-то сумму. Вместе с тем, каждая обслуженная заявка приносит какой-то доход. Умножая этот доход на среднее число заявок А,
обслуживаемых в единицу времени, мы получим средний доход от СМО в единицу времени. Естественно, при увеличении числа каналов этот доход растет, но растут и расходы, связанные с содержанием каналов. Что перевесит — увеличение доходов или расходов? Это зависит от условий операции, от «платы за обслуживание заявки» и от стоимости содержания канала. Зная эти величины, можно найти оптимальное число каналов, наиболее эффективное экономически. Мы такой задачи решать не будем, предоставляя все тому же «неленивому и любопытному читателю» придумать пример и решить. Вообще, придумывание задач больше развивает, чем решение уже поставленных кем-то.
2. Одноканальная СМО с неограниченной очередью. На практике довольно часто встречаются одноканальные СМО с очередью (врач, обслуживающий пациентов; телефон-автомат с одной будкой; ЭВМ, выполняющая заказы пользователей).
В теории массового обслуживания одноканальные СМО с очередью также занимают особое место (именно к таким СМО относится большинство полученных до сих пор аналитических формул для немарковских систем). Поэтому мы уделим одноканальной СМО с очередью особое внимание.
Пусть имеется одноканальная СМО с очередью, на которую не наложено никаких ограничений (ни по длине очереди, ни по времени ожидания). На эту СМО поступает поток заявок с интенсивностью ?; поток обслуживании имеет интенсивность ?, обратную среднему времени обслуживания заявки tоб. Требуется найти финальные вероятности состояний СМО, а также характеристики ее эффективности:
Lсист. — среднее число заявок в системе,
Wсист.— среднее время пребывания заявки в системе,
Lоч — среднее число заявок в очереди,
Wоч — среднее время пребывания заявки в очереди,
Pзан — вероятность того, что канал занят (степень загрузки канала).
Что касается абсолютной пропускной способности А
и относительной Q, то вычислять их нет надобности:
в силу того, что очередь неограниченна, каждая заявка рано или поздно будет обслужена, поэтому А = ?, по той же причине Q = 1.

Рис. 20.2.
Решение. Состояния системы, как и раньше, будем нумеровать по числу заявок, находящихся в СМО:
S0
— канал свободен,
S1 — канал занят (обслуживает заявку), очереди нет,
S2 — канал занят, одна заявка стоит в очереди,
Sk — канал занят, k — 1 заявок стоят в очереди,
Теоретически число состояний ничем не ограничено (бесконечно). Граф состоянии имеет вид, показанный на рис. 20.2. Это — схема гибели и размножения, но с бесконечным числом состояний. По всем стрелкам поток заявок с интенсивностью ? переводит систему слева направо, а справа налево — поток обслуживании с интенсивностью ?.
Прежде всего спросим себя, а существуют ли в этом случае финальные вероятности? Ведь число состояний системы бесконечно, и, в принципе, при t > ? очередь может неограниченно возрастать! Да, так оно и есть: финальные вероятности для такой СМО существуют не всегда, а только когда система не перегружена.
Можно доказать, что если ? строго меньше единицы (?< 1), то финальные вероятности существуют, а при ? ? 1 очередь при t > ? растет неограниченно. Особенно «непонятным» кажется этот факт при ? = 1. Казалось бы, к системе не предъявляется невыполнимых требований: за время обслуживания одной заявки приходит в среднем одна заявка, и все должно быть в порядке, а вот на деле — не так. При ? = 1 СМО справляется с потоком заявок, только если поток этот — регулярен, и время обслуживания — тоже не случайное, равное интервалу между заявками. В этом «идеальном» случае очереди в СМО вообще не будет, канал будет непрерывно занят и будет регулярно выпускать обслуженные заявки. Но стоит только потоку заявок или потоку обслуживании стать хотя бы чуточку случайными — и очередь уже будет расти до бесконечности. На практике этого не происходит только потому, что «бесконечное число заявок в очереди» — абстракция. Вот к каким грубым ошибкам может привести замена случайных величин их математическими ожиданиями!
Но вернемся к нашей одноканальной СМО с неограниченной очередью. Строго говоря, формулы для финальных вероятностей в схеме гибели и размножения выводились нами только для случая конечного числа состояний, но позволим себе вольность — воспользуемся ими и для бесконечного числа состояний. Подсчитаем финальные вероятности состояний по формулам (19.8), (19.7). В нашем случае число слагаемых в формуле (19.8) будет бесконечным. Получим выражение для р0:
p0 = [1 + ?/? + (?/?)2
+... + (?/?)k +.. ]-1
=
= (1 + р + р2 + ... + рk +… .)-1. (20.11)
Ряд в формуле (20.11) представляет собой геометрическую прогрессию. Мы знаем, что при ? < 1 ряд сходится — это бесконечно убывающая геометрическая прогрессия со знаменателем р. При р ? 1 ряд расходится (что является косвенным, хотя и не строгим доказательством того, что финальные вероятности состояний р0, p1, ..., pk, ... существуют только при р<1). Теперь предположим, что это условие выполнено, и ? <1. Суммируя прогрессию в (20.11), имеем
1 + ? + ?2 + ... + ?k + ... =

откуда
p0 = 1 - ?. (20.12)
Вероятности р1, р2, ..., рk, ... найдутся по формулам:
p1 = ?p0, p2 = ?2p0 ,…,pk
= ?p0, ...,
откуда, с учетом (20.12), найдем окончательно:
p1 = ? (1 - ?), p2 = ?2 (1 - ?), . . . , pk = ?k (1 - ?), . . .(20.13)
Как видно, вероятности p0, p1, ..., pk, ... образуют геометрическую прогрессию со знаменателем р. Как это ни странно, максимальная из них р0 — вероятность того, что канал будет вообще свободен. Как бы ни была нагружена система с очередью, если только она вообще справляется с потоком заявок (?<1), самое вероятное число заявок в системе будет 0.
Найдем среднее число заявок в СМО Lсист.. Тут придется немного повозиться. Случайная величина Z — число заявок в системе — имеет возможные значения 0, 1, 2, .... k, ... с вероятностями p0, р1, р2, ..., pk, ... Ее математическое ожидание равно
Lсист = 0 ? p0 +1 ? p1
+ 2 ? p2 +…+k ? pk
+…=

(сумма берется не от 0 до ?, а от 1 до ?, так как нулевой член равен нулю).
Подставим в формулу (20.14) выражение для pk (20.13):
Lсист. =

Теперь вынесем за знак суммы ? (1-?):
Lсист. = ? (1-?)

Тут мы опять применим «маленькую хитрость»: k?k-1 есть не что иное, как производная по ? от выражения ?k; значит,
Lсист. = ? (1-?)

Меняя местами операции дифференцирования п суммирования, получим:
Lсист. = ? (1-?)

Но сумма в формуле (20.15) есть не что иное, как сумма бесконечно убывающей геометрической прогрессии с первым членом ? и знаменателем ?; эта сумма
равна


Lсист =

Ну, а теперь применим формулу Литтла (19.12) и найдем среднее время пребывания заявки в системе:
Wсист
=

Найдем среднее число заявок в очереди Lоч. Будем рассуждать так: число заявок в очереди равно числу заявок в системе минус число заявок, находящихся под обслуживанием.
Значит (по правилу сложения математических ожиданий), среднее число заявок в очереди Lоч равно среднему числу заявок в системе Lсист минус среднее число заявок под обслуживанием. Число заявок под обслуживанием может быть либо нулем (если канал свободен), либо единицей (если он занят). Математическое ожидание такой случайной величины равно вероятности того, что канал занят (мы ее обозначили Рзан). Очевидно, Рзан равно единице минус вероятность р0
того, что канал свободен:
Рзан = 1 - р0
= ?. (20.18)
Следовательно, среднее число заявок под обслуживанием равно
Lоб = ?, (20.19)
отсюда
Lоч = Lсист – ? =

и окончательно
Lоч =

По формуле Литтла (19.13) найдем среднее время пребывания заявки в очереди:

Таким образом, все характеристики эффективности СМО найдены.
Предложим читателю самостоятельно решить пример: одноканальная СМО представляет собой железнодорожную сортировочную станцию, на которую поступает простейший поток составов с интенсивностью ? = 2 (состава в час). Обслуживание (расформирование) состава длится случайное (показательное) время со средним значением tоб =• 20 (мин.). В парке прибытия станции имеются два пути, на которых могут ожидать обслуживания прибывающие составы; если оба пути заняты, составы вынуждены ждать на внешних путях. Требуется найти (для предельного, стационарного режима работы станции): среднее, число составов lсист, связанных со станцией, среднее время Wсист пребывания состава при станции (на внутренних путях, на внешних путях и под обслуживанием), среднее число Lоч составов, ожидающих очереди на расформирование (все равно, на каких путях), среднее время Wоч пребывания состава на очереди. Кроме того, попытайтесь найти среднее число составов, ожидающих расформирования на внешних путях Lвнеш и среднее время этого ожидания Wвнеш (две последние величины связаны формулой Литтла). Наконец, найдите суммарный суточный штраф Ш, который придется заплатить станции за простои составов на внешних путях, если за один час простоя одного состава станция платит штраф а (руб.).
На всякий случай сообщаем ответы: Lсист. = 2 (состава), Wсист. = 1 (час), Lоч = 4/3 (состава), Wоч = 2/3 (часа), Lвнеш = 16/27 (состава), Wвнеш = 8/27 ? 0,297 (часа). Средний суточный штраф Ш за ожидание составов на внешних путях получим, перемножая среднее число составов, прибывающих на станцию за сутки, среднее время ожидания состава на внешних путях и часовой штраф а: Ш ? 14,2а.
3. re-канальная СМО с неограниченной очередью. Совершенно аналогично задаче 2, но чуточку более сложно, решается задача об n-канальной СМО с неограниченной очередью. Нумерация состояний — опять по числу заявок, находящихся в системе:
S0 — в СМО заявок нет (все каналы свободны),
S1 — занят один канал, остальные свободны,
S2 — занято два канала, остальные свободны,
Sk — занято k каналов, остальные свободны,
Sn — заняты все п
каналов (очереди нет),
Sn+1 — заняты все n каналов, одна заявка стоит в очереди,
Sn+r — заняты вес п каналов, r заявок стоит в очереди,
Граф состояний показан на рис. 20.3. Предлагаем читателю самому обдумать и обосновать значения интенсивностей, проставленных у стрелок. Граф рис. 20.3
|
|
|
|
|
|
 |
 |
 |
 |
 |
 |
|||||||||||||||||
 |
 |
 |
 |
 |
 |
pиc. 20.3.
есть схема гибели и размножения, но с бесконечным числом состояний. Сообщим без доказательства естественное условие существования финальных вероятностей: ?/n<1. Если ?/n ? 1, очередь растет до бесконечности.
Предположим, что условие ?/n < 1 выполнено, и финальные вероятности существуют. Применяя все те же формулы (19.8), (19.7) для схемы гибели и размножения, найдем эти финальные вероятности. В выражении для р0 будет стоять ряд членов, содержащих факториалы, плюс сумма бесконечно убывающей геометрической прогрессии со знаменателем ?/n.
Суммируя ее, найдем

Теперь найдем характеристики эффективности СМО. Из них легче всего находится среднее число занятых каналов k == ?/?, = ? (это вообще справедливо для любой СМО с неограниченной очередью). Найдем среднее число заявок в системе Lсист и среднее число заявок в очереди Lоч. Из них легче вычислить второе, по формуле
Lоч =

выполняя соответствующие преобразования по образцу задачи 2
(с дифференцированием ряда), получим:
Lоч =

Прибавляя к нему среднее число заявок под обслуживанием (оно же — среднее число занятых каналов) k = ?, получим:
Lсист = Lоч + ?. (20.24)
Деля выражения для Lоч и Lсист на ?, по формуле Литтла получим средние времена пребывания заявки в очереди и в системе:

А теперь решим любопытный пример. Железнодорожная касса по продаже билетов с двумя окошками представляет собой двухканальную СМО с неограниченной очередью, устанавливающейся сразу к двум окошкам (если одно окошко освобождается, ближайший в очереди пассажир его занимает). Касса продает билеты в два пункта: А и В. Интенсивность потока заявок (пассажиров, желающих купить билет) для обоих пунктов А и В одинакова: ?А = ?В = 0,45 (пассажира в минуту), а в сумме они образуют общий поток заявок с интенсивностью ?А + ?В = 0,9. Кассир тратит на обслуживание пассажира в среднем две минуты. Опыт показывает, что у кассы скапливаются очереди, пассажиры жалуются на медленность обслуживания, Поступило рационализаторское предложение: вместо одной кассы, продающей билеты и в А и в В,
создать две специализированные кассы (по одному окошку в каждой), продающие билеты одна — только в пункт А, другая — только в пункт В.
Разумность этого предложения вызывает споры — кое-кто утверждает, что очереди останутся прежними. Требуется проверить полезность предложения расчетом. Так как мы умеем считать характеристики только для простейших СМО, допустим, что все потоки событий — простейшие (на качественной стороне выводов это не скажется).
Ну, что же, возьмемся за дело. Рассмотрим два варианта организации продажи билетов — существующий и предлагаемый.
Вариант I (существующий). На двухканальную СМО поступает поток заявок с интенсивностью ? = 0,9; интенсивность потока обслуживании ? = 1/2 = 0,5; ? = ?/? = l,8. Так как ?/2 = 0,9<1, финальные вероятности существуют. По первой формуле (20.22) находим р0
? 0,0525. Среднее, число заявок в очереди находим по формуле (20.23): Lоч ? 7,68; среднее время, проводимое заявкой в очереди (по первой из формул (20.25)), равно Wоч ? 8,54 (мин.).
Вариант II (предлагаемый). Надо рассмотреть две одноканальные СМО (два специализированных окошка); на каждую поступает поток заявок с интенсивностью ? = 0,45; ?. по-прежнему равно 0,5; ? = ?/? = 0,9<1; финальные вероятности существуют. По формуле (20.20) находим среднюю длину очереди (к одному окошку) Lоч = 8,1.
Вот тебе и раз! Длина очереди, оказывается, не только не уменьшилась, а увеличилась! Может быть, уменьшилось среднее время ожидания в очереди? Посмотрим. Деля Lоч на ? = 0,45, получим Wоч ? 18 (минут).
Вот так рационализация! Вместо того чтобы уменьшиться, и средняя длина очереди, и среднее время ожидания в ней увеличились!
Давайте попробуем догадаться, почему так произошло? Пораскинув мозгами, приходим к выводу: произошло это потому, что в первом варианте (двухканальная СМО) меньше средняя доля времени, которую простаивает каждый из двух кассиров: если он не занят обслуживанием пассажира, покупающего билет в пункт А, он может заняться обслуживанием пассажира, покупающего билет в пункт В, и наоборот. Во втором варианте такой взаимозаменяемости нет: незанятый кассир просто сидит, сложа руки...
— Ну,
ладно,— готов согласиться читатель,— увеличение можно объяснить, но почему оно такое существенное? Нет ли тут ошибки в расчете?
И на этот вопрос мы ответим. Ошибки нет. Дело в том,
что в нашем примере обе СМО работают на пределе своих возможностей; стоит немного увеличить время обслуживания (т. е. уменьшить ?), как они уже перестанут справляться с потоком пассажиров, и очередь начнет неограниченно возрастать.
А «лишние простои» кассира в каком- то смысле равносильны уменьшению его производительности ?.
Таким образом, кажущийся сначала парадоксальным (или даже просто неверным) результат вычислений оказывается на поверку правильным и объяснимым.
Такого рода парадоксальными выводами, причина которых отнюдь не очевидна, богата теория массового обслуживания. Автору самому неоднократно приходилось «удивляться» результатам расчетов, которые потом оказывались правильными.
Размышляя над последней задачей, читатель может поставить вопрос так: ведь если касса продает билеты только в один пункт, то, естественно, время обслуживания должно уменьшиться, ну, не вдвое, а хоть сколько-нибудь, а мы считали, что оно по-прежнему в среднем равно 2 (мин.). Предлагаем такому придирчивому читателю ответить на вопрос: а насколько надо его уменьшить, чтобы «рационализаторское предложение» стало выгодным? Снова мы встречаемся хотя и с элементарной, но все же задачей оптимизации. С помощью ориентировочных расчетов даже на самых простых, марковских моделях удается прояснить качественную сторону явления — как выгодно поступать, а как — невыгодно. В следующем параграфе мы познакомимся с некоторыми элементарными немарковскими моделями, которые еще расширят наши возможности.
После того, как читатель ознакомился с приемами вычисления финальных вероятностей состояний и характеристик эффективности для простейших СМО (овладел схемой гибели и размножения и формулой Литтла), ему можно предложить для самостоятельного рассмотрения еще две простейшие СМО.
4. Одноканальная СМО с ограниченной очередью. Задача отличается от задачи 2 только тем, что число заявок в очереди ограничено (не может превосходить некоторого заданного т). Если новая заявка приходит в момент, когда все места в очереди заняты, она покидает СМО не обслуженной (получает отказ).
Надо найти финальные вероятности состояний (кстати, они в этой задаче существуют при любом ? — ведь число состояний конечно), вероятность отказа Ротк, абсолютную пропускную способность А, вероятность того, что канал занят Рзан, среднюю длину очереди Lоч, среднее число заявок в СМО Lсист, среднее время ожидания в очереди Wоч, среднее время пребывания заявки в СМО Wсист.
При вычислении характеристик очереди можно пользоваться тем же приемом, какой мы применяли в задаче 2, с той разницей, что суммировать надо не бесконечную прогрессию, а конечную.
5. Замкнутая СМО с одним каналом и m источниками заявок. Для конкретности поставим задачу в следующей форме: один рабочий обслуживает т
станков, каждый из которых время от времени требует наладки (исправления). Интенсивность потока требований каждого работающего станка равна ?. Если станок вышел из строя в момент, когда рабочий свободен, он сразу же поступает на обслуживание. Если он вышел из строя в момент, когда рабочий занят, он становится в очередь и ждет, пока рабочий освободится. Среднее время наладки станка tоб = 1/?. Интенсивность потока заявок, поступающих к рабочему, зависит от того, сколько станков работает. Если работает k станков, она равна k?. Найти финальные вероятности состояний, среднее число работающих станков и вероятность того, что рабочий будет занят.
Заметим, что и в этой СМО финальные вероятности
будут существовать при любых значениях ? и ? = 1/tоб, так как число состояний системы конечно.
§ 21. Более сложные задачи теории массового обслуживания
В этом параграфе мы кратко рассмотрим некоторые вопросы, относящиеся к немарковским СМО. До сих пор все формулы нами выводились или, по крайней мере, могли быть выведены читателем, вооруженным схемой гибели и размножения, формулой Литтла и умением дифференцировать. То, что будет рассказано в данном параграфе, читателю придется принять на веру.
До сих пор мы занимались только простейшими СМО, для которых все потоки событий, переводящий их из состояния в состояние, были простейшими. А как быть, если они не простейшие? Насколько реально это допущение? Насколько значительны ошибки, к которым оно приводит, когда оно нарушается? На все эти вопросы мы попытаемся ответить здесь.
Как это ни грустно, но надо признаться, что в области немарковской теории массового обслуживания похвастать нам особенно нечем. Для немарковских СМО существуют только отдельные, считанные результаты, позволяющие выразить в явном, аналитическом виде характеристики СМО через заданные условия задачи — число каналов, характер потока заявок, вид распределения времени обслуживания.
Приведем некоторые из этих результатов.
1. n-канальная СМО с отказами, с простейшим потоком заявок и произвольным распределением времени обслуживания. В предыдущем параграфе мы вывели формулы Эрланга (20.4), (20.5) для финальных вероятностей состояний СМО с отказами. Сравнительно недавно (в 1959 г.) Б. А. Севастьянов [19] доказал, что эти формулы справедливы не только при показательном, но и при произвольном распределении времени обслуживания.
2. Одноканальная СМО с неограниченной очередью, простейшим потоком заявок и произвольным распределением времени обслуживания. Если на одноканальную СМО с неограниченной очередью поступает простейший поток заявок с интенсивностью ?, а время обслуживания имеет произвольное распределение с математическим ожиданием tоб = 1/?. и коэффициентом вариации v?, то среднее число заявок в очереди равно

а среднее число заявок в системе

где, как и ранее, ? = ?/?.,
a v? — отношение среднего квадратического отклонения времени обслуживания к его математическому ожиданию. Формулы (21.1), (21.2) носят название формул Полячека — Хинчина.
Деля Lоч, и Lсист на ?, получим, согласно формуле Литтла, среднее время пребывания заявки в очереди и среднее время пребывания в системе:


Заметим, что в частном случае, когда время обслуживания — показательное, v? = 1 и формулы (21.1), (21.2) превращаются в уже знакомые нам формулы (20.16), (20.20) для простейшей одноканальной СМО. Возьмем другой частный случай — когда время обслуживания вообще не случайно и v? = 0. Тогда среднее число заявок в очереди уменьшается вдвое по сравнению с простейшим случаем. Это и естественно: если обслуживание заявки протекает более организованно, «регулярно», то СМО работает лучше, чем при плохо организованном, беспорядочном обслуживании.
3. Одноканальная СМО с произвольным потоком заявок и произвольным распределением времени обслуживания. Рассматривается одноканальная СМО с неограниченной очередью, на которую поступает произвольный рекуррентный поток заявок с интенсивностью ? и коэффициентом вариации v? интервалов между заявками, заключенным между нулем и единицей: 0 < v? < 1.
Время обслуживания Тоб также имеет произвольное распределение со средним значением tоб = 1/? и коэффициентом вариации v?, тоже заключенным между нулем и единицей. Для этого случая точных аналитических формул получить не удается;
можно только приближенно оценить среднюю длину очереди, ограничить ее сверху и снизу.
Доказано, что в этом случае

Если входящий поток — простейший, то обе оценки — верхняя и нижняя — совпадают, и получается формула Полячека — Хинчина (21.1). Для грубо приближенной оценки средней длины очереди М. А. Файнбергом (см. [18]) получена очень простая формула:

Среднее число заявок в системе получается из Lоч простым прибавлением ? — среднего числа обслуживаемых заявок:
Lсист = Lоч + ?. (21.7)
Что касается средних времен пребывания заявки в очереди и в системе, то они вычисляются через Lоч и Lсист по формуле Литтла делением на ?.
Таким образом, характеристики одноканальных СМО с неограниченной очередью могут быть (если не точно, то приближенно) найдены и в случаях, когда потоки заявок и обслуживании не являются простейшими.
Возникает естественный вопрос: а как же обстоит дело с многоканальными немарковскими СМО? Со всей откровенностью ответим: плохо. Точных аналитических методов для таких систем не существует. Единственное, что мы всегда можем найти, это среднее число занятых каналов k = ?. Что касается Lоч, Lсист, Wоч, Wсист, то для них таких общих формул написать не удается.
Правда, если каналов действительно много (4—5 или больше), то непоказательное время обслуживания не страшно: был бы входной поток простейшим. Действительно, общий поток «освобождений» каналов складывается из потоков освобождений отдельных каналов, а в результате такого наложения («суперпозиции») получается, как мы знаем, поток, близкий к простейшему. Так что в этом случае замена непоказательного распределения времени обслуживания показательным приводит к сравнительно малым ошибкам.
К счастью, входной поток заявок во многих задачах практики близок к простейшему.
Хуже обстоит дело, когда входной поток заведомо не простейший. Ну, в этом случае приходится пускаться на хитрости. Например, подобрать две одноканальные СМО, из которых одна по своей эффективности заведомо «лучше» данной многоканальной, а другая — заведомо «хуже» (очередь больше, время ожидания больше). А для одноканальной СМО мы худо-бедно уже умеем находить характеристики в любом случае.
Как же подобрать такие одноканальные СМО — «лучшую» и «худшую»? Это можно сделать по-разному. Оказывается, заведомо худший вариант можно получить, если расчленить данную n-канальную СМО на п
одноканальных, а общий поступающий на них простейший поток распределять между этими одноканальными СМО в порядке очереди: первую заявку — в первую СМО, вторую — во вторую и т. д. Мы знаем, что при этом на каждую СМО будет поступать поток Эрланга n-го порядка, с коэффициентом вариации, равным 1/




Обе характеристики будут меньше, чем для исходной n-канальной СМО (будут представлять собой «оптимистические» оценки). От них, деля на ?, можно перейти к «оптимистическим» оценкам для времени пребывания в СМО и в очереди.
ГЛАВА 7
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ (МЕТОД МОНТЕ-КАРЛО)
§ 22. Идея, назначение и область применимости метода
В предыдущих главах мы научились строить некоторые аналитические модели операций со стохастической («доброкачественной») неопределенностью. Эти модели позволяют установить аналитическую (формульную) зависимость между условиями операции, элементами решения и результатом (исходом) операции, который характеризуется одним пли несколькими показателями эффективности. Во многих операциях системы массового обслуживания или другие, аналогичные им (например, технические устройства с узлами, выходящими из строя), фигурируют как «подсистемы» или «части» общей управляемой системы. Польза и желательность построения аналитических моделей (хотя бы приближенных) сомнению не подлежат. Беда в том, что их удается построить только для самых простых, «незатейливых» систем, и, самое главное, они требуют допущения о марковском характере процесса, что далеко не всегда соответствует действительности. В случаях, когда аналитические методы неприменимы (или же требуется проверить их точность), приходится прибегать к универсальному методу статистического моделирования или, как его часто называют, методу Монте-Карло.
Идея метода чрезвычайно проста и состоит она в следующем. Вместо того чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. В действительности конкретное осуществление (реализация) случайного процесса складывается каждый раз по-иному; так же и в результате статистического моделирования («розыгрыша») мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса.
Что она может нам дать? Сама по себе — почти ни чего, так же как, скажем, один случай излечения больного с помощью какого-то лекарства (или несмотря на лекарство). Другое дело, если таких реализации получено много. Это множество реализации можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики. После такой обработки могут быть получены (разумеется, приближенно) любые интересующие нас характеристики: вероятности событий, математические ожидания и дисперсии случайных величин и, т. д. При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования, заставляем ее «работать на нас».
Нередко такой прием оказывается проще, чем попытки построить аналитическую модель. Для сложных операций, в которых участвует большое число элементов (машин, людей, организаций, подсобных средств), в которых случайные факторы сложно переплетены, где процесс — явно немарковский, метод статистического моделирования, как правило, оказывается проще аналитического (а нередко бывает и единственно возможным).
В сущности, методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета. Приведем пример, когда метод Монте-Карло возможен, но крайне неразумен. Пусть, например, по какой-то цели производится три независимых выстрела, из которых каждый попадает в цель с вероятностью 1/2. Требуется найти вероятность хотя бы одного попадания. Элементарный расчет дает нам вероятность хотя бы одного попадания равной 1 - (1/2)3 = 7/8. Ту же задачу, в принципе, можно решить и «розыгрышем», статистическим моделированием. Вместо «трех выстрелов» будем бросать «три монеты», считая, скажем, герб — за «попадание», решку — за «промах». Опыт считается «удачным», если хотя бы на одной из монет выпадет герб. Произведем очень-очень много опытов, подсчитаем общее количество «удач» и разделим на число N
произведенных опытов. Таким образом, мы получим частоту события, а она при большом числе опытов близка к вероятности. Ну, что же? Применить такой прием мог бы разве человек, вовсе не знающий теории вероятностей, тем не менее, в принципе, он возможен1).
А теперь возьмем другую задачу. Пусть работает многоканальная СМО с очередью, но процесс, протекающий в ней, явно немарковский: промежутки между заявками имеют непоказательное распределение, время обслуживания — тоже. Мало того: каналы время от времени выходят из строя и начинают ремонтироваться; как время безотказной работы канала, так и время ремонта — непоказательные. Требуется найти характеристики СМО: вероятности состояний как функции времени, среднюю длину очереди, среднее время пребывания заявки в системе и т. д. Задача, казалось бы, не такая уж сложная. Однако любой человек, сколько-нибудь знакомый с теорией массового обслуживания, не колеблясь, выберет для ее решения метод статистического моделирования (перспективы создания обозримой аналитической модели здесь, прямо сказать, неважные). Ему придется разыграть множество реализации случайного процесса (разумеется, на ЭВМ, а не вручную) и из такой искусственной «статистики» найти приближенно интересующие его вероятности (как частоты соответствующих событий) и математические ожидания (как средние арифметические значений случайных величин).
В задачах исследования операций метод Монте-Карло применяется в трех основных ролях:
1) при моделировании сложных, комплексных операций, где присутствует много взаимодействующих случайных факторов;
2) при проверке применимости более простых, аналитических методов и выяснении условий их применимости;
3) в целях выработки поправок к аналитическим формулам типа «эмпирических формул» в технике.
В § 3 (глава 1) мы уже говорили в общих чертах о сравнительных достоинствах и недостатках аналитических и статистических моделей. Теперь мы можем уточнить: основным недостатком аналитических моделей является то, что они неизбежно требуют каких-то допущении, в частности, о «марковости» процесса.
1) Нечто похожее иногда случается, когда люди, мало знакомые с теорией вероятностей, моделируют методом Монте–Карло задачи, имеющие аналитическое решение.
Приемлемость этих допущений далеко не всегда может быть оценена без контрольных расчетов, а производятся они методом Монте-Карло. Образно говоря, метод Монте-Карло в задачах исследования операций играет роль своеобразного ОТК. Статистические модели не требуют серьезных допущений и
упрощений. В принципе, в статистическую модель «лезет» что угодно — любые законы распределения, любая сложность системы, множественность ее состояний. Главный же недостаток статистических моделей — их громоздкость и трудоемкость. Огромное число реализации, необходимое для нахождения искомых параметров с приемлемой точностью, требует большого расхода машинного времени. Кроме того, результаты статистического моделирования гораздо труднее осмыслить, чем расчеты по аналитическим моделям, и соответственно труднее оптимизировать решение (его приходится «нащупывать» вслепую). Правильное сочетание аналитических и статистических методов в исследовании операций — дело искусства, чутья и опыта исследователя. Нередко аналитическими методами удается описать какие-то «подсистемы», выделяемые в большой системе, а затем из таких моделей, как из «кирпичиков», строить здание большой, сложной модели.
§ 23. Единичный жребий и формы его организации
Основным элементом, из совокупности, которых складывается статистическая модель, является одна случайная реализация моделируемого явления, например, «один случай работы машины до ее отказа», «один день работы промышленного цеха», «одна эпидемия» и т. д. Реализация — это как бы один «экземпляр» случайного явления со всеми присущими ему случайностями. Реализации отличаются друг от друга за счет этих случайностей.
Отдельная реализация разыгрывается с помощью специально разработанной процедуры (алгоритма), в которой важную роль играет «бросание жребия». Каждый раз, когда в ход явления вмешивается случай, его влияние учитывается не расчетом, а жребием.
Поясним понятие «жребия». Пусть в ходе процесса наступил момент, когда его дальнейшее развитие (а значит и результат) зависит от того, произошло или нет какое-то событие А? Например, попал ли в цель снаряд? Исправна ли аппаратура? Обнаружен ли объект? Устранена ли неисправность? Тогда нужно «бросанием жребия» решить вопрос: произошло событие или нет. Как можно осуществить этот жребий? Нужно привести в действие какой-то механизм случайного выбора (например, бросание монеты или игральной кости, или же вынимание жетона с цифрой из вращающегося барабана, или выбор наугад какого-то числа из таблицы). Нам хорошо знакомы некоторые механизмы случайного выбора (например, «пляска шариков» перед объявлением выигравших номеров «Спортлото»). Если жребий бросается для того, чтобы узнать, произошло ли событие А,
его нужно организовать так, чтобы условный результат розыгрыша имел ту же вероятность, что и событие А. Как это делается—мы увидим ниже. Кроме случайных событий, на ход и исход операции могут влиять различные случайные величины, например: время до первого отказа технического устройства;
время обслуживания заявки каналом СМО; размер детали; вес поезда, прибывающего на участок пути; координаты точки попадания снаряда и т. п. С помощью жребия можно разыграть и значение любой случайной величины, и совокупность значений нескольких.
Условимся называть «единичным жребием» любой опыт со случайным исходом, который отвечает на один из следующих вопросов:
1. Произошло или нет событие Л?
2. Какое из событий А1, А2, .. .,
Аk произошло?
3. Какое значение приняла случайная величина X?
4. Какую совокупность значений приняла система случайных величин X1, Х2, .. ., Хk?
Любая реализация случайного явления методом Монте-Карло строится из цепочки единичных жребиев, перемежающихся с обычными расчетами. Ими учитывается влияние исхода жребия на дальнейший ход событий (в частности, на условия, в которых будет разыгран следующий жребий).
Единичный жребий может быть разыгран разными способами, но есть один стандартный механизм, с помощью которого можно осуществить любую разновидность жребия.
А именно, для каждой из них достаточно уметь получать случайное число R, все значения
 |
1. Произошло или нет событие А? Чтобы ответить на этот вопрос, надо знать вероятность р события А. Разыграем случайное число R
от 0 до 1, и если оно оказалось меньше p, как показано на рис. 23.1, будем считать, что событие произошло, а если больше р — не произошло.
А как быть, — спросит читатель, — если число R оказалось в точности равным p? Вероятностью такого совпадения можно пренебречь. А уж если оно случилось, можно поступать как угодно: или всякое «равно» считать за «больше», или за «меньше», или попеременно за то и другое — от этого результат моделирования практически не зависит.
2. Какое из нескольких событий появилось? Пусть события А1, A2, ..., Аk несовместны и образуют полную группу. Тогда сумма их вероятностей р1, р2, ..., pk равна единице. Разделим интервал (0, 1) на k, участков длиной p1, р2,…, pk (рис. 23.2). На какой из участков попало число R — то событие и появилось.
3. Какое значение приняла случайная величина X?
Если случайная величина Х дискретна, т. е. имеет значения х1, x2, ..., xk с вероятностями р1, р2, ..., pk, то, очевидно, случай сводится к предыдущему. Теперь рассмотрим случай, когда случайная величина непрерывна и имеет заданную плотность вероятности f(x). Чтобы разыграть ее значение, достаточно осуществить следующую процедуру: перейти от плотности вероятности f(x) к функции распределения F(r) по формуле

затем найти для функции F
обратную ей функцию ?. Затем разыграть случайное число R от 0 до 1 и взять от него эту обратную функцию:
X=?(R). (23.2)
Можно доказать (мы этого делать не будем), что полученное значение Х имеет как раз нужное нам распределение f(x).
 |
от 0 до 1 и для него ищется такое значение X,
при котором F(X) = R
(это показано стрелками на рис. 23.3).
Рис. 23.3. |
Z = R1, + R2 + ... + R6 (23.3)
имеет распределение, настолько близкое к нормальному, что в большинстве практических задач им можно заменить нормальное. Для того чтобы математическое ожидание и среднее квадратическое отклонение этого нормального распределения были равны заданным mx, ox, нужно подвергнуть величину Z линейному преобразованию и вычислить.
Х =

Это и будет нужная нам нормально распределенная случайная величина.
4. Какую совокупность значений приняли случайные величины Х1, Х2,...,Хk? Если случайные величины независимы, то достаточно k раз повторить процедуру, описанную в предыдущем пункте. Если же они зависимы, то разыгрывать каждую последующую нужно на основе ее условного закона распределения при условии, что все предыдущие приняли те значения, которые дал розыгрыш (более подробно останавливаться на этом случае мы не будем).
Таким образом, мы рассмотрели все четыре варианта единичного жребия и убедились, что все они сводятся к розыгрышу (одно- или многократному) случайного числа R от 0 до 1.
Возникает вопрос: а как же разыгрывается это число R? Существует целый ряд разновидностей так называемых «датчиков случайных чисел», решающих эту задачу. Остановимся вкратце на некоторых из них.
Самый простой из датчиков случайных чисел — это вращающийся барабан, в котором перемешиваются перенумерованные шарики (или жетоны). Пусть, например, нам надо разыграть случайное число R от 0 до 1 с точностью до 0,001. Заложим в барабан 1000 перенумерованных шариков, приведем его во вращение и после остановки выберем первый попавшийся шарик, прочтем его номер и разделим на 1000.
Можно поступить и немного иначе: вместо 1000 шариков заложить в барабан только 10, с цифрами 0, 1,2,..., 9. Вынув один шарик, прочтем первый десятичный знак дроби. Вернем его обратно, снова покрутим барабан и возьмем второй шарик — это будет второй десятичный знак и т. д. Легко доказать (мы этого делать не будем), что полученная таким образом десятичная дробь будет иметь равномерное распределение от 0 до 1. Преимущество этого способа в том, что он никак не связан с числом знаков, с которым мы хотим знать R.
Отсюда один шаг до рационализаторского предложения: не разыгрывать число R каждый раз, когда это понадобится, а сделать это заранее, т. е. составить достаточно обширную таблицу, в которой все цифры 0, 1, 2, .... 9 встречаются случайным образом и с
одинаковой вероятностью (частотой). До этого приема люди давно додумались: такие таблицы действительно составлены и применяются на практике. Они называются таблицами случайных чисел. Выдержки из таблиц случайных чисел приводятся во многих руководствах по теории вероятностей и математической статистике (например, [201]). Краткие выдержки из таблиц случайных чисел приведены и в популярной книжке автора [21], где, кстати, даны и примеры моделирования случайных процессов с помощью таблиц случайных чисел.
При ручном применении метода Монте-Карло таблицы случайных чисел — наилучший способ розыгрыша случайного числа R от 0 до 1. Если же моделирование осуществляется не вручную, а на ЭВМ, то пользование таблицами случайных чисел (как и вообще таблицами) нерационально — они слишком загрузили бы память.
Для розыгрыша R на ЭВМ применяются специальные датчик и, которыми оснащены многие вычислительные машины. Это могут быть как «физические датчики», основанные на преобразовании случайных шумов, так и вычислительные алгоритмы, по которым сама машина вычисляет так называемые «псевдослучайные числа». Приставка «псевдо» означает «как бы», «якобы». И в самом деле, числа, вычисляемые с помощью таких алгоритмов, фактически случайными не являются, но практически ведут себя как случайные; все значения от 0 до 1 встречаются в среднем одинаково часто и, кроме того, связь между последовательными значениями получаемых чисел практически отсутствует. Существует ряд алгоритмов вычисления псевдослучайных чисел, различающихся между собой по простоте, равномерности и другим признакам (см. [22]). Один из самых простых алгоритмов вычисления псевдослучайных чисел состоит в следующем. Берут два произвольных n-значных двоичных числа а1 и a2, перемножают их и в полученном произведении берут п средних знаков; это будет число a3. Затем перемножают a1 и а2,
в произведении снова берут п
средних знаков и т. д. Полученные таким образом числа рассматривают как последовательность двоичных дробей с п
знаками после запятой. Такая последовательность дробей ведет себя практически как ряд значения случайного числа R
от 0 до 1. Существуют и другие алгоритмы, основанные' не на перемножении, а на «суммировании со сдвигом». Подробнее останавливаться на конкретных алгоритмах получения псевдослучайных чисел не имеет смысла: в настоящее время практически все ЭВМ снабжены либо датчиками случайных чисел, либо проверенными алгоритмами вычисления псевдослучайных1).
§ 24. Определение характеристик стационарного случайного процесса по одной реализации
В исследовании операций нередко приходится встречаться с задачами, где случайный процесс продолжается достаточно долго в одинаковых условиях, и нас как раз интересуют характеристики этого процесса в предельном, установившемся режиме. Например, железнодорожная сортировочная станция работает круглосуточно, и интенсивность потока составов, прибывающих на нее, почти не зависит от времени.
В качестве других примеров систем, в которых случайный процесс довольно быстро переходит в устойчивое состояние, можно назвать ЭВМ, линии связи, технические устройства, непрерывно эксплуатируемые и т. п.
О предельном, стационарном режиме и предельных (финальных) вероятностях состояний мы уже говорили в главе 5 (§ 17) в связи с марковскими случайными процессами. Существуют ли они для немарковских процессов? Да, в известных случаях существуют и не зависят от начальных условий. При решении вопроса о том, существуют ли они для данной задачи, можно в первом приближении поступать так: заменить мысленно все потоки событий простейшими; если для этого случая окажется, что финальные вероятности существуют, то они будут существовать и для немарковского процесса. Если это так, то для предельного, стационарного режима все вероятностные характеристики можно определить методом Монте-Карло не по множеству реализации, а всего по одной, но достаточно длинной реализации. В этом случае одна длинная реализация дает такую же информацию о свойствах процесса, что и множество реализации той же общей продолжительности.
1) Этот довод подозрительно напоминает рассуждения г-жи Простаковой («Недоросль» Фонвизина) по поводу ненужности изучения географии: «Да извозчики-то на что? Это их дало. Это и наука-то не дворянская. Дворянин только скажи: повези меня туда, свезут, куда изволишь».
 |
Тогда интересующие нас вероятности состояний можно найти, как долю времени, которую система проводит в этих состояниях, а средние значения случайных величин получить усреднением не по множеству реализации, а по времени, вдоль peaлизации.
Рис. 24.1
Рассмотрим пример. Моделируется методом Монте-Карло работа немарковской одноканальной СМО с очередью. Число мест в очереди ограничено двумя. Заявка, пришедшая в момент, когда оба места в очереди заняты, покидает СМО не обслуженной (получает отказ).
Время от времени канал может выходить из строя. Если канал вышел из строя, находившиеся в СМО заявки (как под обслуживанием, так и в очереди), не покидают СМО, а ожидают конца ремонта. Все потоки событий не простейшие, а произвольные рекуррентные. Возможные состояния СМО:
S0i — канал исправлен, в системе i заявок,
S1i — канал ремонтируется, в системе i заявок (i = 0, 1, 2,3).
Граф состояний СМО показан на рис. 24.1. Из вида графа заключаем, что финальные вероятности существуют. Предположим, что моделирование работы СМО методом Монте-Карло на большом промежутке времени Т
произведено. Требуется найти характеристики эффективности СМО: Ротк — вероятность того, что заявка покинет СМО не обслуженной, Риспр
— вероятность того, что канал исправен, А —
абсолютную пропускную способность СМО, Lсист — среднее число заявок в СМО, Lоч — среднее число заявок в очереди, Wсист и Wоч — среднее время пребывания заявки в системе и в очереди.
Сначала найдем финальные вероятности состояний р00,p01, p02, p03, p10, p11, p12, p13.Для этого нужно вдоль реализации подсчитать суммарное время, которое система находится в каждом из состоянии: T00, Т01, T02, Т03, Т10, T11, Т12, Т13, и разделить каждое из них на время Т. Получим:

Вероятность отказа равна вероятности того, что заявка придет в момент, когда в СМО уже находятся три заявки:
Ротк = p03 + p13.
Абсолютная пропускная способность равна
А = ? (1 – Ротк),
где ? — интенсивность потока заявок.
Вероятность того, что канал исправен, получим, суммируя все вероятности, у которых первый индекс равен нулю:
Pиспр = p00
+ p01 + p02 + p03.
Среднее число заявок в СМО подсчитаем, умножая возможные числа заявок в СМО на соответствующие вероятности и складывая:
Lсист = 1 (p01 + p11) + 2 (p02 + p12) + 3 (p03 + p13).
Это равносильно тому, как если бы мы отметили на оси времени отрезки, на которых в СМО находится 0, 1, 2, 3 заявки и суммарную длительность участков умножили соответственно на 1, 2, 3, сложили и разделили на Т.
Среднее число заявок в очереди Lоч получим, вычитая из Lсист среднее число заявок под обслуживанием (для одноканальной СМО это вероятность того, что канал занят):
Рзан = 1 - (p00 + p10).
Среднее время пребывания заявки в системе и в очереди получим по формуле Литтла:

На этом мы, заканчиваем краткое наложение метода Монте-Карло, отсылая интересующегося читателя к руководствам [6, 22], где он изложен более полно и где, в частности, рассматривается вопрос о точности статистического моделирования.
ГЛАВА 8
ИГРОВЫЕ МЕТОДЫ ОБОСНОВАНИЯ РЕШЕНИЙ
§ 25. Предмет и задачи теории игр
В предыдущих трех главах мы рассматривали вопросы, связанные с математическим моделированием (а иногда и оптимизацией решений), в случаях, когда условия операции содержат неопределенность, но относительно «доброкачественную», стохастическую, которая в принципе может быть учтена, если знать законы распределения (на худой конец — числовые характеристики) фигурирующих в задаче случайных факторов.
Такая неопределенность—еще «полбеды». В этой главе мы рассмотрим (по необходимости бегло) гораздо худший вид неопределенности (в § 5 мы назвали ее «дурной»), когда некоторые параметры, от которых зависит успех операции, неизвестны, и нет никаких данных, позволяющих судить о том, какие их значения более, а какие — менее вероятны. Неопределенными (в «дурном» смысле) могут быть как внешние, «объективные» условия операции, как и «субъективные» — сознательные действия противников, соперников или других лиц. Как известно, «чужая душа — потемки», и предсказывать, как себя поведут эти лица, еще труднее, чем предсказывать в области случайных явлений.
Разумеется, когда речь идет о неопределенной (в «дурном» смысле) ситуации, выводы, вытекающие из научного исследования, не могут быть ни точными, ни однозначными. Но и в этом случае количественный анализ может принести пользу при выборе решения.
Такого рода задачами занимается специальный раздел математики, носящий причудливое название «теория игр и статистических решений».
В некоторых (редких) случаях разработанные в нем методы дают возможность фактически найти оптимальное решение. Гораздо чаще эти методы позволяют попросту глубже разобраться в ситуации, оценить каждое решение с различных (иногда противоречивых) точек зрения, взвесить его преимущества и недостатки и, в конце концов, принять решение, если не единственно правильное, то, по крайней мере, до конца продуманное. Нельзя забывать, что при выборе решения в условиях неопределенности неизбежен некоторый произвол и элемент риска. Недостаток информации — всегда беда, а не преимущество (хотя именно при отсутствии информации исследователь может щегольнуть наиболее тонкими математическими методами). Тем не менее, в сложной ситуации, плохо обозримой в целом, когда, как говорится, «рябит в глазах» от подробностей, всегда полезно представить варианты в такой форме, чтобы сделать произвол выбора менее грубым, а риск — по возможности минимальным. Нередко задача ставится так: какой ценой можно заплатить за недостающую информацию, чтобы за ее счет повысить эффективность операции? Заметим, что иногда для выбора решения и не требуется точной информации об условиях, а достаточно только указать «район», в котором они находятся (метод «районирования» И. Я. Динера, см. [23]).
В данной главе излагаются некоторые минимальные сведения из теории игр и статистических решений. Для более подробного ознакомления с нею можно рекомендовать работы [24—281].
Наиболее простыми из ситуаций, содержащих «дурную» неопределенность, являются так называемые конфликтные ситуации. Так называются ситуации, в которых сталкиваются интересы двух (или более) сторон, преследующих разные (иногда противоположные) цели, причем выигрыш каждой стороны зависит от того, как себя поведут другие.
Примеры конфликтных ситуаций многообразны. К ним, безусловно, принадлежит любая ситуация, складывающаяся в ходе боевых действий, ряд ситуаций в области экономики (особенно в условиях капиталистической конкуренции). Столкновение противоречащих друг другу интересов наблюдается также в судопроизводстве, в спорте, видовой борьбе.
В какой- то мере противоречивыми являются также взаимоотношения различных ступеней иерархии в сложных системах. В некотором смысле «конфликтной* можно считать и ситуацию с несколькими критериями: каждый из них предъявляет к управлению свои требования и, как правило, эти требования противоречивы.
Теория игр представляет собой математическую теорию конфликтных ситуаций. Ее цель — выработка рекомендаций по разумному поведению участников конфликта.
Каждая непосредственно взятая из практики конфликтная ситуация очень сложна, и ее анализ затруднен наличием привходящих, несущественных факторов. Чтобы сделать возможным математический анализ конфликта, строится его математическая модель, Такую модель называют игрой.
От реального конфликта игра отличается тем, что ведется по определенным правилам. Эти правила указывают «права и обязанности» участников, а также исход игры — выигрыш или проигрыш каждого участника в зависимости от сложившейся обстановки. Человечество издавна пользуется такими формализованными моделями конфликтов — «играми» в буквальном смысле слова (шашки, шахматы, карточные игры и т. п.). Отсюда и название «теории игр», и ее терминология: конфликтующие стороны условно называются «игроками», одно осуществление игры — «партией», исход игры — «выигрышем» или «проигрышем». Мы будем считать, что выигрыши (проигрыши) участников имеют количественное выражение (если это не так, то всегда можно им его приписать, например, в шахматах считать «выигрыш» за единицу, «проигрыш» — за минус единицу, «ничью» — за нуль).
В игре могут сталкиваться интересы двух или более участников; в первом случае игра называется «парной», во втором — «множественной». Участники множественной игры могут образовывать коалиции (постоянные или временные). Одна из задач теории игр — выявление разумных коалиций во множественной игре и правил обмена информацией между участниками. Множественная игра с двумя постоянными коалициями, естественно, обращается в парную.
Развитие игры во времени можно представлять как ряд последовательных «ходов» участников.
Ходом называется выбор игроком одного из предусмотренных правилами игры действий и его осуществление. Ходы бывают личные и случайные. При личном ходе игрок сознательно выбирает и осуществляет тот или другой вариант действий (пример — любой ход в шахматах). При случайном ходе выбор осуществляется не волей игрока, а каким-то механизмом случайного выбора (бросание монеты, игральной кости, вынимание карты из колоды и т. п.). Некоторые игры (так называемые «чисто азартные») состоят только из случайных ходов — ими теория игр не занимается. Ее цель — оптимизация поведения игрока в игре, где (может быть, наряду со случайными) есть личные ходы. Такие игры называются стратегическими.
Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации.
Обычно, участвуя в игре, игрок не следует каким-либо жестким, «железным» правилам: выбор (решение) принимается им в ходе игры, когда он непосредственно наблюдает ситуацию. Однако теоретически дело не изменится, если предположить, что все эти решения приняты игроком заранее («если сложится такая-то ситуация, я поступлю так-то»). Это будет значить, что игрок выбрал определенную стратегию. Теперь он может и не участвовать в игре лично, а передать список правил незаинтересованному лицу (судье). Стратегия также может быть задана машине-автомату в виде программы (именно так играют в шахматы ЭВМ).
В зависимости от числа стратегий игры делятся на «конечные» и «бесконечные». Игра называется конечной, если у каждого игрока имеется в распоряжении только конечное число стратегий (в противном случае игра называется бесконечной). Бывают игры (например, шахматы), где в принципе число стратегий конечно, но так велико, что полный их перебор практически невозможен.
Оптимальной стратегией игрока называется такая, которая обеспечивает ему наилучшее положение в данной игре, т. е. максимальный выигрыш. Если игра повторяется неоднократно и содержит, кроме личных, еще и случайные ходы, оптимальная стратегия обеспечивает максимальный средний выигрыш.
Задача теории игр — выявление оптимальных стратегий игроков. Основное предположение, исходя из которого находятся оптимальные стратегии, состоит в том, что противник (в общем случае — противники) по меньшей мере так же разумен, как и сам игрок, и делает все для того, чтобы добиться своей цели. Расчет на разумного противника — лишь одна из возможных позиций в конфликте, но в теории игр именно она кладется в основу.
Игра называется игрой с нулевой суммой, если сумма выигрышей всех игроков равна нулю (т. е. каждый игрок выигрывает только за счет других). Самый простой случай — парная игра с нулевой суммой — называется антагонистической (или и г-рой со строгим соперничеством). Теория антагонистических игр — наиболее развитый раздел теории игр, с четкими рекомендациями. Ниже мы познакомимся с некоторыми ее понятиями и приемами.
Теория игр, как и всякая математическая модель, имеет свои ограничения. Одним из них является предположение о полной («идеальной») разумности противника (противников). В реальном конфликте зачастую оптимальная стратегия состоит в том, чтобы угадать, в чем противник «глуп», и воспользоваться этой глупостью в свою пользу. Схемы теории игр не включают элементов риска, неизбежно сопровождающего разумные решения в реальных конфликтах. В теории игр выявляется наиболее осторожное, «перестраховочное» поведение участников конфликта. Сознавая эти ограничения и поэтому, не придерживаясь слепо рекомендаций, полученных игровыми методами, можно все, же разумно использовать аппарат теории игр как «совещательный» при выборе решения (подобно тому, как молодой, энергичный полководец может прислушаться к мнению умудренного опытом, осторожного старца).
§ 26. Антагонистические матричные игры
Самым простым случаем, подробно разработанным в теории игр, является конечная парная игра с нулевой суммой (антагонистическая игра двух лиц или двух коалиций). Рассмотрим такую игру G, в которой участвуют два игрока А и В, имеющие противоположные интересы: выигрыш одного равен проигрышу другого.
Так как выигрыш игрока А равен выигрышу игрока В с обратным знаком, мы можем интересоваться только выигрышем а
игрока А. Естественно, А хочет максимизировать, а В — минимизировать а. Для простоты отождествим себя мысленно с одним из игроков (пусть это будет А)
и будем его называть «мы», а игрока В —
«противник» (разумеется, никаких реальных преимуществ для А из этого не вытекает). Пусть у нас имеется т возможных стратегий А1, A2, ..., Аm, а у противника — n возможных стратегий В1, В2, ..; Вn (такая игра называется игрой т × n). Обозначим аij наш выигрыш в случае, если мы пользуемся стратегией Ai, а противник—стратегией Bj.
Таблица 26.1
 Bj |
B1 |
B2 |
… |
Bn |
|
A1 A2 … Am |
a11 a21 … am1 |
a21 a … am |
… … … … |
a1n a2n … amn |
выигрыш (или средний выигрыш) a,j нам известен. Тогда в принципе можно составить прямоугольную таблицу (матрицу), в которой перечислены стратегии игроков и соответствующие выигрыши (см. таблицу 26.1).
Если такая таблица составлена, то говорят, что игра G приведена к матричной форме (само по себе приведение игры к такой форме уже может составить трудную задачу, а иногда и практически невыполнимую, из-за необозримого множества стратегий). Заметим, что если игра приведена к матричной форме, то многоходовая игра фактически сведена к одноходовой — от игрока требуется сделать только один ход: выбрать стратегию. Будем кратко обозначать матрицу игры (aij).
Рассмотрим пример игры G (4×5) в матричной форме. В нашем распоряжении (на выбор) четыре стратегии, у противника — пять стратегий. Матрица игры дана в таблице 26.2
Давайте, поразмышляем о том, какой стратегией нам (игроку А)
воспользоваться? В матрице 26.2 есть соблазнительный выигрыш «10»; нас так и тянет выбрать стратегию А3,
при которой этот «лакомый кусок» нам достанется. Но постойте: противник тоже не дурак! Если мы выберем стратегию А3,
он, назло нам, выберет стратегию В3,
и мы получим какой-то жалкий выигрыш «1». Нет, выбирать стратегию А3 нельзя! Как же быть? Очевидно, исходя из принципа осторожности (а он — основной принцип теории игр), надо выбрать

|
Bj Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
|
A1 A2 A3 A4 |
3 1 10 4 |
4 8 3 5 |
5 4 1 3 |
2 3 7 4 |
3 4 6 8 |
Это — так называемый «принцип минимакса»: поступай так, чтобы при наихудшем для тебя поведении противника получить максимальный выигрыш.
Перепишем таблицу 26.2 и в правом добавочном столбце запишем минимальное значение выигрыша в каждой строке, (минимум строки); обозначим его для i-й строки ?i (см. таблицу 26.3).
Таблица 26.3
 Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
?i |
|
A1 A2 A3 A4 |
3 1 10 4 |
4 8 3 5 |
5 4 1 3 |
2 3 7 4 |
3 4 6 8 |
2 1 1 3 |
|
?j |
10 |
8 |
5 |
7 |
8 |
Теперь станем на точку зрения противника и порассуждаем за него. Он ведь не пешка какая-нибудь, а тоже разумен! Выбирая стратегию, он хотел бы отдать поменьше, но должен рассчитывать на наше, наихудшее для него, поведение. Если он выберет стратегию В1, мы ему ответим А3, и он отдаст 10; если выберет B2 — мы ему ответим А2, и он отдаст 8 и т. д. Припишем к таблице 26.3 добавочную нижнюю строку и в ней запишем максимумы столбцов ?j.
Очевидно, осторожный противник должен выбрать ту стратегию, при которой эта величина минимальна (соответствующее значение 5 выделено в таблице 26.3). Эта величина ? — то значение выигрыша, больше которого заведомо не отдаст нам разумный противник. Она называется верхней ценой игры (или «минимаксом» — минимальный из максимальных выигрышей). В нашем примере ? = 5 и достигается при стратегии противника B3.
Итак, исходя из принципа осторожности (перестраховочного правила «всегда рассчитывай на худшее!»), мы должны выбрать стратегию А4,
а противник — стратегию В3.
Такие стратегии называются «минимаксными» (вытекающими из принципа минимакса). До тех пор, пока обе стороны в нашем примере будут придерживаться своих минимаксных стратегий, выигрыш будет равен а43
= 3.
Теперь представим себе на минуту, что мы узнали о том, что противник придерживается стратегии В3. А ну-ка, накажем его за это и выберем стратегию А1 — мы получим 5, а это не так уж плохо. Но ведь противник — тоже не промах; пусть он узнал, что наша стратегия А1;
он тоже поторопится выбрать В4,
сведя наш выигрыш к 2, и т. д. (партнеры «заметались по стратегиям»). Одним словом, минимаксные стратегии в нашем примере неустойчивы по отношению к информации о поведении другой стороны; эти стратегии не обладают свойством равновесия.
Всегда ли это так? Нет, не всегда. Рассмотрим пример с матрицей, данной в таблице 26.4.
В этом примере нижняя Цена игры равна верхней: ? = ? = 6. Что из этого вытекает? Минимаксные стратегии игроков А и В будут устойчивыми. Пока оба игрока их придерживаются, выигрыш равен 6. Посмотрим, что будет, если мы (А) узнаем, что противник (В)
Таблица 26.4
 Ai |
B1 |
B2 |
B3 |
B4 |
?i |
|
A1 A2 A3 |
2 7 5 |
4 6 3 |
7 8 4 |
5 7 1 |
2 6 1 |
|
?j |
7 |
6 |
8 |
7 |
может только ухудшить наше положение.
Равным образом, информация, полученная противником, не заставит его отступить от своей стратегии В2. Пара стратегий А2, B2 обладает свойством равновесия (уравновешенная пара стратегий), а выигрыш (в нашем случае 6), достигаемый при этой паре стратегий, называется «седловой точкой матрицы» 1). Признак наличия седловой точки и уравновешенной пары стратегий — это равенство нижней и верхней цены игры; общее значение ? и ? называется ценой игры. Мы будем обозначать его v:
? = ? = v
Стратегии Ai, Bj (в данном случае А2, В2), при которых этот выигрыш достигается, называются оптимальными чистыми стратегиями, а их совокупность — решением игры. Про саму игру в этом случае говорят, что она решается в чистых стратегиях. Обеим сторонам А
и В можно указать их оптимальные стратегии, при которых их положение — наилучшее из возможных. А что игрок А при этом выигрывает 6, а игрок В — проигрывает 6,— что же, Таковы условия игры: они выгодны для А и невыгодны для В
1) Термин «седловая точка» взят из геометрии — так называется точка на поверхности, где одновременно достигается минимум по одной координате и максимум по другой.
У читателя может возникнуть вопрос: а почему оптимальные стратегии называются «чистыми»? Несколько забегая вперед, ответим на этот вопрос: бывают стратегии «смешанные», состоящие в том, что игрок применяет не одну какую-то стратегию, а несколько, перемежая их случайным образом. Так вот, если допустить кроме чистых еще и смешанные стратегии, всякая конечная игра имеет решение — точку равновесия. Но об атом речь еще впереди.
Наличие седловой точки в игре — это далеко не правило, скорее — исключение. Большинство игр не имеет седловой точки. Впрочем, есть разновидность игр, которые всегда имеют седловую точку и, значит, решаются в чистых стратегиях. Это — так называемые «игры с полной информацией». Игрой с полкой информацией называется такая игра, в которой каждый игрок при каждом личном ходе знает всю предысторию ее развития, т.
е. результаты всех предыдущих ходов, как личных, так и случайных. Примерами игр с полной информацией могут служить: шашки, шахматы, «крестики и нолики» и т. п.
В теории игр доказывается, что каждая игра с полной информацией имеет седловую точку, и значит, решается в чистых стратегиях. В каждой игре с полной информацией существует пара оптимальных стратегий, дающая устойчивый выигрыш, равный цепе игры v. Если такая игра состоит только из личных ходов, то при применении каждым игроком своей оптимальной стратегии она должна кончаться вполне определенным образом — выигрышем, равным цене игры. А значит, если решение игры известно, самая игра теряет смысл!
Возьмем элементарный пример игры с полной информацией: два игрока попеременно кладут пятаки на круглый стол, выбирая произвольно положение центра монеты (взаимное перекрытие монет не разрешается). Выигрывает тот, кто положит последний пятак (когда места для других уже не останется). Легко убедиться, что исход этой игры, в сущности, предрешен. Есть определенная стратегия, обеспечивающая выигрыш тому из игроков, кто кладет монету первым. А именно, он должен первый раз положить пятак о центре стола, а затем на каждый ход противника отвечать симметричным ходом. Очевидно, как бы ни вел себя противник, ему не избежать проигрыша. Точно так же обстоит дело и с шахматами и вообще играми с полной информацией: любая из них, записанная в матричной форме, имеет седловую точку, и значит, решение в чистых стратегиях, а, следовательно, имеет смысл только до тех пор, пока это решение не найдено. Скажем, шахматная игра либо всегда кончается выигрышем белых, либо всегда —
выигрышем черных, либо всегда —
ничьей, только чем именно — мы пока не знаем (к счастью для любителей шахмат). Прибавим еще: вряд ли будем знать и в обозримом будущем, ибо число стратегий так огромно, что крайне трудно (если не невозможно) привести игру к матричной форме и найти в ней седловую точку.
А теперь спросим себя, как быть, если игра не имеет седловой точки: ? ? ? ? Ну что же, если каждый игрок вынужден выбрать одну - единственную чистую стратегию, то делать нечего: надо руководствоваться принципом минимакса.
Другое дело, если можно скоп стратегии «смешивать», чередовать случайным образом с какими-то вероятностями. Применение смешанных стратегий мыслится таким образом: игра повторяется много раз; перед каждой партией игры, когда игроку предоставляется личный ход, он «передоверяет» свой выбор случайности, «бросает жребий», и берет ту стратегию, которая выпала (как организовать жребий, мы уже знаем из предыдущей главы).
Смешанные стратегии в теории игр представляют собой модель изменчивой, гибкой тактики, когда ни один из игроков не знает, как поведет себя противник в данной партии. Такая тактика (правда, обычно безо всяких математических обоснований) часто применяется в карточных играх. Заметим при этом, что лучший способ скрыть от противника свое поведение — это придать ему случайный характер и, значит, самому не знать заранее, как ты поступишь.
Итак, поговорим о смешанных стратегиях. Будем обозначать смешанные стратегии игроков А и В
соответственно SA =•(p1, р2,
..., pm), SB = (q1, q2, …, qn), где p1, p2, …, pm (образующие в сумме единицу) — вероятности применения игроком А стратегий А1, A2,…, Am; q1, q2, …, qn —вероятности применения игроком В стратегий В1, В2, ..., Вn. В частном случае, когда все вероятности, кроме одной, равны нулю, а эта одна — единице, смешанная стратегия превращается в чистую.
Существует основная теорема теории игр: любая конечная игра двух лиц с нулевой суммой имеет, по крайней мере, одно решение — пару оптимальных стратегий, в общем случае смешанных

Пара оптимальных стратегий

0, то игра выгодна для нас, если v<0 — для противника; при v = 0 игра «справедливая», одинаково выгодная для обоих участников.
Рассмотрим пример игры без седловой точки и приведем (без доказательства) ее решение. Игра состоит в следующем: два игрока А и В одновременно и не сговариваясь показывают один, два или три пальца. Выигрыш решает общее количество пальцев: если оно четное, выигрывает А и получает у В сумму, равную этому числу; если нечетное, то, наоборот, А
платит В сумму, равную этому числу. Как поступать игрокам?
Составим матрицу игры. В одной партии у каждого игрока три стратегии: показать один, два или три пальца. Матрица 3×3 дана в таблице 26.5; в дополнительном правом столбце приведены минимумы строк, а в дополнительной нижней строке — максимумы столбцов.
Нижняя цена игры ? = — 3 и соответствует стратегии A1. Это значит, что при разумном, осторожном поведении мы гарантируем, что не проиграем больше, чем 3. Слабое утешение, но все же лучше, чем, скажем, выигрыш — 5, встречающийся в некоторых клетках матрицы. Плохо нам, игроку А...
Но утешимся:
положение противника, кажется, еще хуже: нижняя цена игры ? = 4, т. е. при разумном поведении он отдаст нам минимум 4. В общем, положение не слишком хорошее — ни для той, ни для другой стороны. Но посмотрим: нельзя ли его улучшить? Оказывается, можно. Если каждая сторона будет применять не одну какую-то чистую стратегию, а смешанную, в которую
Таблица 26.5
 Ai |
B1 |
B2 |
B3 |
?i |
|
A1 A2 A3 |
2 -3 4 |
-3 4 -5 |
4 -5 6 |
-3 -5 -5 |
|
?j |
4 |
4 |
6 |

то средний выигрыш будет устойчиво равен нулю (значит, игра «справедлива» и одинаково выгодна той и другой стороне). Стратегии

§ 27. Методы решения конечных игр
Перед тем, как решать игру m×n, нужно, прежде всего, попытаться ее упростить, избавившись от лишних стратегий.
Это делается подобно тому, как мы когда-то отбрасывали заведомо невыгодные решения в § 6. Введем понятие «доминирования». Стратегия Ai игрока А
называется доминирующей над стратегией Аk, если в строке Ai стоят выигрыши не меньшие, чем в соответствующих клетках строки Ak, и из них по крайней мере один действительно больше, чем в соответствующей клетке строки Аk. Если все выигрыши строки Ai, равны соответствующим выигрышам строки Ak, то стратегия Аi называется дублирующей стратегию Ak. Аналогично определяются доминирование и дублирование для стратегий игрока В:
доминирующей называется та его стратегия, при которой везде стоят выигрыши не большие, чем в соответствующих клетках другой, и по крайней мере один из них действительно меньше; дублирование означает полное повторение одного столбца другим. Естественно, что если для какой-то стратегии есть доминирующая, то эту стратегию можно отбросить; также отбрасываются и дублирующие стратегии.
Поясним сказанное примером. Пусть игра 5×5 задана матрицей таблицы 27.1.
Таблица 27.1
 Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
|
A1 A2 A3 A4 A5 |
4 3 4 3 3 |
7 5 4 6 5 |
2 6 2 1 6 |
3 8 2 2 8 |
4 9 8 4 9 |
значит А1 доминирует над A4. Отбросим A4 и получим матрицу 3×5 (таблица 27.2).
Но это еще не все! Приглядевшись к таблице 27.2, замечаем, что в ней некоторые стратегии игрока В доминируют над другими: например, B3 над B4, и В5,
a B1 — над стратегией В2 (не забудьте, что В стремится отдать поменьше!).
Таблица 27.2
 Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
|
A1 A2 A3 |
4 3 4 |
7 5 4 |
2 6 2 |
3 8 2 |
4 9 8 |
Отбрасывая столбцы B2, В4, В5, получаем игру 3×2 (таблица 27.3).
Наконец, в таблице 27.3 строка А3
дублирует А1, поэтому ее можно отбросить. Окончательно получим игру 2×2 (таблица 27.4).

|
Bj Ai |
B1 |
B3 |
|
A1 A2 A3 |
4 3 4 |
2 6 2 |
 Ai |
B1 |
B3 |
|
A1 A2 |
4 3 |
2 6 |
В руководствах по теории игр обычно останавливаются на решении простейших игр 2×2, 2×п и т×2,
которое допускает геометрическую интерпретацию, но мы этого делать не будем — сразу возьмем «быка за рога» и покажем, как можно решить любую игру т×п.
Пусть имеется игра т×п без седловой точки с матрицей (аij) (см. таблицу 27.5).
Таблица 27.5
 Bj |
B1 |
B2 |
… |
Bn |
|
A1 A2 … Am |
a11 a21 … am1 |
a12 a22 … am2 |
… … … … |
a1n a2n … amn |

Мы хотим найти решение игры, т. е. две оптимальные смешанные стратегии

дающие каждой стороне максимально возможный для нее средний выигрыш (минимальный проигрыш).
Найдем сначала

Заставим противника (В)
отступать от своей оптимальной стратегии, пользуясь чистыми стратегиями В1, B2, ..., Вn (а мы тем временем упорно держимся стратегии


Разделим неравенства (27.2) на положительную величину v
и введем обозначения:

Тогда условия (27.2) примут вид

где x1, x2,..., xm — неотрицательные переменные. В силу (27.3) и того, что p1 + р2 + ... + рm = 1, переменные x1, x2,..., хm удовлетворяют условию
х1, + х2, + ... + xm =

Но v есть не что иное, как наш гарантированный выигрыш, естественно, мы хотим сделать его максимальным, а значит, величину

Таким образом, задача решения игры свелась к математической задаче: найти неотрицательные значения переменных х1, х2, ..., xm такие, чтобы они удовлетворяли линейным ограничениям-неравенствам (27.4) и обращали в минимум линейную функцию этих переменных:
L = х1, + х2, + ... + xm => min. (27.6)
«Ба! — скажет читатель, — что-то знакомое!» И точно — перед нами не что иное, как задача линейного программирования. Таким образом, задача решения игры т×п свелась к задаче линейного программирования с n ограничениями-неравенствами и т переменными. Зная x1, x2, ..., xm, можно по формулам (27.3) найти p1, р2, ..., рm и, значит, оптимальную стратегию

Оптимальная стратегия игрока В находится совершенно аналогично, с той разницей, что В
стремится минизировать, а не максимизировать выигрыш, а значит, обратить не в минимум, а в максимум величину


Таким образом, решение игры m×п
эквивалентно решению задачи линейного программирования. Нужно заметить, что и наоборот, — для любой задачи линейного программирования может быть построена эквивалентная ей задача теории игр (на том, как это делается, мы останавливаться не будем). Эта связь задач теории игр с задачами линейного программирования оказывается полезной не только для теории игр, но и для линейного программирования. Дело в том, что существуют приближенные численные методы решения игр, которые в некоторых случаях (при большой размерности задачи) оказываются проще, чем «классические» методы линейного программирования.
Опишем один из самых простых численных методов решения игр — так называемый метод итераций (иначе — метод Брауна — Робинсон). Идея его в следующем. Разыгрывается «мысленный эксперимент», в котором стороны А
и В поочередно применяют друг против друга свои стратегии, стремясь выиграть побольше (проиграть поменьше). Эксперимент состоит из ряда «партий» игры. Начинается он с того, что один из игроков (скажем, А) выбирает произвольно одну из своих стратегий Ai. Противник (В) отвечает ему той из своих стратегий Bj которая хуже всего для А, т. е.
обращает его выигрыш при стратегии 4, в минимум. Дальше снова очередь А —он отвечает В той своей стратегией Аk, которая дает максимальный выигрыш при стратегии Вj противника. Дальше — снова очередь противника. Он отвечает нам той своей стратегией, которая является наихудшей не для последней, примененной нами, стратегии Аk, а для смешанной стратегии, в которой до сих пор примененные стратегии Ai, Ak встречаются с равными вероятностями. И так далее: на каждом шаге итерационного процесса каждый игрок отвечает на очередной ход другого той своей стратегией, которая является оптимальной для него относительно смешанной стратегии другого, в которую все примененные до сих пор стратегии входят пропорционально частотам их применения. Вместо того чтобы вычислять каждый раз средний выигрыш, можно пользоваться просто «накопленным» за предыдущие ходы выигрышем и выбирать ту свою стратегию, при которой этот накопленный выигрыш максимален (минимален).
Доказано, что такой метод сходится: при увеличении числа «партий» средний выигрыш на одну партию будет стремиться к цене игры, а частоты применения стратегий — к их вероятностям в оптимальных смешанных стратегиях игроков.
Впрочем, лучше всего можно понять итерационный метод на конкретном примере. Продемонстрируем его на примере игры 3×3 предыдущего параграфа (таблица 26.5). Чтобы не иметь дела с отрицательными числами, прибавим к элементам матрицы таблицы 26.5 число 5 (см. таблицу 27.6); при этом цена игры увеличится на 5, а решение

Начнем с произвольно выбранной стратегии игрока А, —
например, со стратегии А3. В таблице 27.7 приведены первые 15 шагов итерационного процесса по методу Брауна — Робинсон (читатель может самостоятельно продолжить расчеты).
Таблица 27.6
 Ai |
B1 |
B2 |
B3 |
|
A1 A2 A3 |
7 2 9 |
2 9 0 |
9 0 11 |
в данной партии (получается прибавлением элементов соответствующей строки к тому, что было строкой выше). Из этих накопленных
выигрышей в таблице 27.7 подчеркнут минимальный (если их несколько, подчеркиваются все). Подчеркнутое число определяет ответный выбор игрока В в данной партии — он выбирает ту стратегию, которая соответствует подчеркнутому числу (если их несколько, берется любая). Таким образом определяется номер j оптимальной (в данной партии) стратегии В (ставится в следующем столбце). В последующих
Таблица 27.7
|
k |
i |
B1 |
B2 |
B3 |
j |
A1 |
A2 |
A3 |
 |
 |
 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
3 2 2 2 1 3 1 2 2 1 3 2 2 1 3 |
9 11 13 15 22 31 38 40 42 49 58 60 62 69 78 |
0 9 18 27 29 29 31 40 49 51 51 60 69 71 71 |
11 11 11 11 20 31 40 40 40 49 60 60 60 69 80 |
2 2 3 3 3 2 2 2 3 1 2 2 3 1 2 |
2 4 13 22 31 33 35 37 46 53 55 57 66 73 75 |
9 18 18 18 18 27 36 45 45 47 56 65 65 67 76 |
0 0 11 2 33 33 33 33 44 53 53 53 64 73 73 |
0 4,5 3,67 2,75 4,00 4,84 4,43 5,00 4,45 4,90 4,64 5,00 4,61 4,93 4,74 |
9 9 6 5,50 6,60 5,50 5,14 5,61 5,11 5,30 5,09 5,41 5,07 5,21 5,06 |
4,5 6,75 4,84 4,13 5,30 5,17 4,79 5,30 4,78 5,10 4,87 5,20 4,84 5,07 4,90 |
трех столбцах дается накопленный выигрыш за k партий соответственно при стратегиях А1, А2, А3
игрока А (получается прибавлением элементов столбца Вj к тому, что было строкой выше). Из этих значений в таблице 27.7 «надчеркнуто» максимальное; оно определяет выбор стратегии игрока А в следующей партии (строкой ниже). В последних трех столбцах таблицы 27.7 даны:


v* — среднее арифметическое между ними (оно служит лучше, чем нижняя и верхняя, приближенной оценкой цены игры).
Как видно, величина v* незначительно колеблется около цены игры v = 5 (цена исходной игры была 0, но мы прибавили к элементам матрицы по 5). Подсчитаем по таблице 27.7 частоты


что не так уж сильно отличается от вероятностей p1, p2, p3, q1, q2, q3, равных, как мы указывали раньше, для первой, второй и третьей стратегий соответственно 1/4 = 0,25, 1/2 = 0,50, 1/4 = 0,25. Такие сравнительно хорошие приближения мы получили уже при 15 итерациях — это обнадеживает! К сожалению, дальше процесс приближений будет идти не так резво. Сходимость метода Брауна — Робинсон, как показывает опыт, очень медленная, Существуют способы, позволяющие как бы «подхлестнуть» еле плетущийся процесс, но мы на них останавливаться не будем.
Очень важным преимуществом итерационного метода решения игр является то, что его трудоемкость сравнительно медленно возрастает с увеличением размерности игры т×п, тогда как трудоемкость метода линейного программирования растет при увеличении размерности задачи гораздо быстрее.
* * *
Таким образом, читатель получил некоторое представление о теории антагонистических игр и о методах решения матричных игр.
Скажем несколько критических слов по поводу этой теории и ее практической значимости. В свое время, когда теория игр еще только появилась, на нее возлагались большие надежды в смысле выбора решений для конфликтных ситуаций.
Эти надежды оправдались лишь в малой степени.
Прежде всего, на практике не так уж часто встречаются строго антагонистические конфликты — разве только в настоящих «играх» (шашки, шахматы, карты и т. п.). Вне этих искусственных ситуаций, где одна сторона стремится, во что бы то ни стало обратить выигрыш в максимум, а другая — в минимум, такие конфликты почти не встречаются. Казалось бы, где, как не в области боевых действий должна была бы с успехом применяться теория игр? Ведь здесь мы встречаемся с самыми «свирепыми» антагонизмами, с самой резкой противоположностью интересов! Но оказывается, что конфликтные ситуации в этой области сравнительно редко удается свести к парным играм с нулевой суммой. Схема строгого антагонизма применима, как правило, только к операциям малого масштаба, ограниченным по значению. Например, сторона А — группа самолетов, налетающих на объект, сторона В — средства противовоздушной обороны объекта; первая стремится максимизировать вероятность уничтожения объекта, вторая — ее минимизировать. Здесь схема парной игры с нулевой суммой может найти применение. Но возьмем чуть более сложный пример: две группировки боевых единиц (типа танков, самолетов, кораблей) ведут бой. Каждая сторона стремится поразить как можно больше боевых единиц противника. В этом примере антагонизм ситуации теряет свою чистоту: она уже не сводится к парной игре с нулевой суммой. Если цели участников конфликта не прямо противоположны, а просто не совпадают, математическая модель становится много сложнее: мы уже не можем интересоваться выигрышем только одной стороны; возникает так называемая «биматричная игра», где каждый из участников стремится максимизировать свой выигрыш, а не просто минимизировать выигрыш противника. Теория таких игр гораздо сложнее, чем теория антагонистических игр, а главное, из этой теории не удается получить четких рекомендаций по оптимальному образу действий сторон [26].
Второе критическое замечание будет касаться понятия «смешанных стратегий». Если речь идет о многократно повторяемой ситуации, в которой каждая сторона может легко (без дополнительных затрат) варьировать свое поведение от случая к случаю, оптимальные смешанные стратегии в самом деле могут повысить средний выигрыш.
Но бывают ситуации, когда решение надо принять одно-единственное (например, выбрать план строительства системы оборонительных сооружений). Разумно ли будет «передоверить свой выбор случаю»,— грубо говоря, бросить монету, и если выпал герб, выбрать первый вариант плана, а если решка — второй? Вряд ли найдется такой руководитель, который в сложной и ответственной ситуации решится делать выбор случайным образом, хотя бы это и вытекало из принципов теории игр!
Наконец, последнее соображение: в теории игр считается, что каждому игроку известны все возможные стратегии противника, неизвестно лишь то, какой именно из них он воспользуется в данной партии игры. В реальном конфликте это обычно не так: перечень возможных стратегий противника как раз неизвестен, и наилучшим решением в конфликтной ситуации нередко будет именно выйти за пределы известных противнику стратегий, «ошарашить» его чем-то совершенно новым, непредвиденным!
Как видно из вышеизложенного, теория игр в качестве основы для выбора решения (даже в остроконфликтной ситуации) имеет много слабых мест. Значит ли это, что ее не нужно изучать, что она вовсе не нужна в исследовании операций? Нет, не значит. Теория игр ценна, прежде всего, самой постановкой задач, которая учит, выбирая решение в конфликтной ситуации, не забывать о том, что противник тоже мыслит, и учитывать его возможные хитрости и уловки. Пусть рекомендации, вытекающие из игрового подхода, не всегда определенны и не всегда осуществимы — все же полезно, выбирая решение, ориентироваться, в числе других, и па игровую модель. Не надо только выводы, вытекающие из этой модели, считать окончательными и непререкаемыми 1).
1) Изложенная здесь точка зрения автора на роль и значение теории игр вовсе на общепринята. Некоторые авторы, напротив, считают игровые подходы в исследовании операций основными (см., например, [28]).
§ 28. Задачи теории статистических решений
Близкой по идеям и методам к теории игр является теория статистических решений.
От теории игр она отличается тем, что неопределенная ситуация не имеет конфликтной окраски — никто никому не противодействует, но элемент неопределенности налицо. В задачах теории статистических решений неизвестные условия операции зависят не от сознательно действующего «противника» (или других участников конфликта), а от объективной действительности, которую в теории статистических решений принято называть «природой». Соответствующие ситуации часто называются «играми с природой». «Природа» мыслится как некая незаинтересованная инстанция («равнодушная природа»,— по Пушкину), «поведение» которой неизвестно, но, во всяком случае, не злонамеренно.
Казалось бы, отсутствие сознательного противодействия упрощает задачу выбора решения. Оказывается, нет: не упрощает, а усложняет. Правда, принимающему решение в «игре с природой» в самом деле «легче» добиться успеха (ведь ему никто не мешает!), но ему «труднее» обосновать свой выбор. В игре против сознательного противника элемент неопределенности отчасти снимается тем, что мы «думаем» за противника, «принимаем» за него решение, самое неблагоприятное для нас самих. В игре же с природой такая концепция не подходит: кто ее знает, как она, матушка, себя поведет? Поэтому теория статистических решений — наиболее «шаткая» в смысле рекомендаций наука. Все же у нее есть право на существование и на внимание со стороны лиц, занимающихся исследованием операций.
Рассмотрим игру с природой: у нас (сторона А) имеется m возможных стратегий А1, А2, ..., Am; что касается обстановки, то о ней можно сделать п предположений: П1, П2, ..., Пn. Рассмотрим их как «стратегии природы». Наш выигрыш aij при каждой паре стратегий Ai,Пj задан матрицей (таблица 28.1).
Требуется выбрать такую стратегию игрока А
(чистую или, может быть, смешанную, если это возможно), которая является более выгодной по сравнению с другими.
С первого взгляда кажется, что эта задача похожа на игру двух игроков А и П с противоположными интересами и должна решаться теми же методами.
Но это не совсем так. Отсутствие противодействия со стороны природы делает ситуацию качественно другой1).
Таблица 28.1
 Ai |
П1 |
П2 |
… |
Пn |
|
A1 A2 … Am |
a11 a21 … am1 |
a12 a22 … am2 |
… … … … |
a1n a2n … amn |
превосходит другие («доминирует» над ними), как, например, стратегия Л а в таблице 28.2. Здесь выигрыш при стратегии Ад при любом состоянии природы не меньше, чем при других стратегиях, а при некоторых — больше; значит, все ясно, и нужно выбирать именно эту стратегию.
Таблица 23.2
 Ai |
П1 |
П2 |
П3 |
П4 |
|
A1 A2 A3 А4 |
1 7 3 7 |
2 4 4 4 |
3 4 4 2 |
5 5 1 2 |
Если даже в матрице игры с природой нет одной доминирующей над всеми другими, все же полезно посмотреть, нет ли в ней дублирующих стратегий и уступающих другим при всех условиях (как мы это делали, упрощая матрицу игры). Но здесь есть одна тонкость: так мы можем уменьшить только число стратегий игрока А, но не игрока П — ему ведь все равно, много или мало мы выиграем! Предположим, что «чистка» матрицы произведена, и ни дублирующих, ни заведомо невыгодных игроку А
стратегий в ней нет.
Чем же все-таки руководствоваться при выборе решения? Вполне естественно, должна учитываться матрица выигрышей (аij). Однако в каком-то смысле картина ситуации, которую дает матрица (aij), неполна и не отражает должным образом достоинств и недостатков каждого решения.
Поясним эту ( далеко не простую) мысль. Предположим, что выигрыш aij при нашей стратегии Ai и состоянии природы Пj больше, чем при нашей стратегии Ak и состоянии природы Пl: aij > akl. Но за счет чего больше? За счет того, что мы удачно выбрали стратегию Ai? Необязательно. Может быть, просто состояние природы Пj выгоднее нам, чем Пl. Например, состояние природы «нормальные условия» для любой операции выгоднее, чем «наводнение», «землетрясение» и т. п. Желательно ввести такие показатели, которые не просто давали бы выигрыш при данной стратегии в каждой ситуации, но отражали бы «удачность» или «неудачность» выбора данной стратегии в данной ситуации.
С этой целью в теории решений вводится понятие «риска». Риском rij игрока A при пользовании стратегией Ai в условиях Пj называется разность между выигрышем, который мы получили бы, если бы знали условия Пj, и выигрышем, который мы получим, не зная их и выбирая стратегию Ai.
Очевидно, если бы мы (игрок A) знали состояние природы Пj, мы выбрали бы ту стратегию, при которой наш выигрыш максимален. Этот выигрыш, максимальный в столбце Пj, мы уже раньше встречали и обозначили ?о. Чтобы получить риск rij, нужно из ?j вычесть фактический выигрыш aij:
rij = ?j – aij.
Для примера возьмем матрицу выигрышей (aj) (таблица 28.3) и построим для нее матрицу рисков (rij) (таблица 28.4).
При взгляде на матрицу рисков (таблица 28.4) нам становятся яснее некоторые черты данной «игры с природой». Так, в матрице выигрышей (aij) (таблица 28.3) во второй строке первый и последний элементы были равны друг другу: а21 = а24 = 3.
Таблица 28.3
 Ai |
П1 |
П2 |
П3 |
П4 |
|
А1 А2 А3 |
1 3 4 |
4 8 6 |
5 4 6 |
9 3 2 |
|
?j |
4 |
8 |
6 |
9 |
 Ai |
П1 |
П2 |
П3 |
П4 |
|
А1 А2 А3 |
3 1 0 |
4 0 2 |
1 2 0 |
0 6 7 |
е. выбор стратегии А2
очень плох. Риск—это «плата за отсутствие информации»: в таблице 28.4 r21 = 1, r24 = 6 (тогда как выигрыши аij в том и другом случае одинаковы). Естественно, нам хотелось бы минимизировать риск, сопровождающий выбор решения.
Итак, перед нами — две постановки задачи о выборе решения: при одной нам желательно получить максимальный выигрыш, при другой — минимальный риск.
Мы знаем, что самый простой случай неопределенности — это «доброкачественная» или стохастическая неопределенность, когда состояния природы имеют какие-то вероятности Q1, Q2, .., Qn и эти вероятности нам известны. Тогда естественно (со всеми оговорками, сделанными по этому поводу в § 5) выбрать ту стратегию, для которой среднее значение выигрыша, взятое по строке, максимально:

Любопытно отметить, что та же стратегия, которая обращает в максимум средний выигрыш, обращает в минимум и средний риск:

так что в случае стохастической неопределенности оба подхода («от выигрыша» и «от риска») дают одно в то же оптимальное решение.
Давайте чуточку «испортим» нашу неопределенность и допустим, что вероятности Q1, Q2, …, Qn в принципе существуют, но нам неизвестны. Иногда в этом случае предполагают все состояния природы равновероятными (так называемый «принцип недостаточного основания» Лапласа), но вообще-то это делать не рекомендуется. Все-таки обычно более или менее ясно, какие состояния более, а какие — менее вероятны. Для того чтобы найти ориентировочные значения вероятностей Q1, Q2, ..., Qn, можно, например, воспользоваться методом экспертных оценок (см. § 5). Хоть какие-то ориентировочные значения вероятностей состояний природы все же лучше, чем полная неизвестность. Неточные значения вероятностей состояний природы в дальнейшем могут быть «скорректированы» с помощью специально поставленного эксперимента. Эксперимент может быть как «идеальным», полностью выясняющим состояние природы, так и неидеальным, где вероятности состоянии уточняются по косвенным данным.
Каждый эксперимент, разумеется, требует каких-то затрат, и возникает вопрос: окупаются ли эти затраты возрастанием эффективности? Оказывается, «идеальный» эксперимент имеет смысл проводить только в случае, когда его стоимость меньше, чем минимальный средний риск (см., например, [6]).
Однако не будем больше заниматься случаем стохастической неопределенности, а возьмем случай «дурной неопределенности», когда вероятности состояний природы либо вообще не существуют, либо не поддаются оценке даже приближенно. Ну что же? Обстановка неблагоприятна для принятия «хорошего» решения — попытаемся найти хотя бы не самое худшее.
Здесь все зависит от точки зрения на ситуацию, от позиции исследователя, от того, какими бедами грозит неудачный выбор решения. Опишем несколько возможных подходов, точек зрения (или, как говорят, несколько «критериев» для выбора решения).
1. Максиминный критерий Вальда. Согласно этому критерию игра с природой ведется как игра с разумным, причем агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оптимальной считается стратегия, при которой гарантируется выигрыш в любом случае не меньший, чем «нижняя цена игры с природой»:

Если руководствоваться этим критерием, олицетворяющим «позицию крайнего пессимизма», надо всегда ориентироваться на худшие условия, зная наверняка, что «хуже этого не будет». Очевидно, такой подход — «перестраховочный», естественный для того, кто очень боится проиграть,— не является единственно возможным, но как крайний случай он заслуживает рассмотрения.
2. Критерий минимаксного риска Сэвиджа. Этот критерий — тоже крайне пессимистический, но при выборе оптимальной стратегии советует ориентироваться не на выигрыш, а на риск. Выбирается в качестве оптимальной та стратегия, при которой величина риска в наихудших условиях минимальна:
S
=

Сущность такого подхода в том, чтобы всячески избегать большого риска при принятии решения. В смысле «пессимизма» критерий Сэвиджа сходен с критерием Вальда, но самый «пессимизм» здесь понимается по-другому.
3. Критерий пессимизма-оптимизма Гурвица. Этот критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом («всегда рассчитывай на худшее!»), ни крайним, легкомысленным оптимизмом («авось кривая вывезет!»). Согласно этому критерию выбирается стратегия из условия

где

«коэффициент пессимизма», выбираемый между нулем и единицей. При



выбирается из субъективных соображений — чем опаснее ситуация, чем больше мы хотим в ней «подстраховаться», чем менее наша склонность к риску, тем ближе к единице выбирается

При желании можно построить критерий, аналогичный Н,
исходя не из выигрыша, а из риска, но мы на этом не будем останавливаться.
«Что же,— спросит читатель,— выбор критерия — субъективен, выбор коэффициента

В какой-то мере читатель прав — выбор решения в условиях неопределенности всегда условен, субъективен. И все же в какой-то (ограниченной) мере математические методы полезны и тут. Прежде всего, они позволяют привести игру с природой к матричной форме, что далеко не всегда бывает просто, особенно когда стратегий много (в наших примерах их было очень мало). Кроме того, они позволяют заменить простое лицезрение матрицы выигрышей (или рисков), от которого, когда матрица велика, может просто «зарябить в глазах», последовательным численным анализом ситуации с разных точек зрения, выслушать рекомендации каждой из них и, наконец, остановиться на чем-то определенном. Это аналогично обсуждению вопроса с различных позиций, а в споре, как известно, рождается истина.
Так что не ждите от теории решений окончательных, непререкаемых рекомендаций — единственное, чем она может помочь — это советом...
Если рекомендации, вытекающие из различных критериев, совпадают — тем лучше, значит, можно смело выбрать рекомендуемое решение: оно, скорее всего «не подведет». Если же, как это часто бывает, рекомендации противоречат друг другу, не надо забывать, что у нас голова на плечах. Задумаемся над этими рекомендациями, выясним, насколько к разным результатам они приводят, уточним свою точку зрения и произведем окончательный выбор. Не надо забывать, что в любых задачах обоснования решений некоторый произвол неизбежен — хотя бы при построении математической модели, выборе показателя эффективности. Вся математика, применяемая в исследовании операций, не отменяет этого произвола, а позволяет только «поставить его на свое место».
Таблица 28.5
 Ai |
П1 |
П2 |
П3 |
|
А1 А2 А3 А4 |
20 75 25 85 |
30 20 80 5 |
15 25 35 45 |
Теперь попробуем помочь себе, пользуясь критериями Вальда, Сэпиджа и Гурвица, причем в последнем возьмем

1. Слово имеет критерий Вальда. Подсчитаем минимумы по строкам (см. таблицу 28.6) и выберем ту стратегию, при которой минимум строки максимален (равен 25). Это—стратегия A3.
Таблица 28.6
 Ai |
П1 |
П2 |
П3 |
?i |
|
А1 А2 А3 А4 |
20 75 25 85 |
30 20 80 5 |
15 25 35 45 |
15 20 25 5 |
Из чисел правого столбца минимальное (60) соответствует стратегиям А2
и А3; значит, обе они оптимальны по Сэвиджу.
Таблица 28.7
 Ai |
П1 |
П2 |
П3 |
?i |
|
А1 А2 А3 А4 |
20 75 25 85 |
30 20 80 5 |
15 25 35 45 |
65 60 60 75 |





Максимальное значение hi = 47 соответствует стратегии A3.
Итак, в данном случае все три критерия согласно говорят в пользу стратегии А3, которую есть все основания выбрать.
Таблица 28.8
 Ai |
П1 |
П2 |
П3 |
?i |
 |
hi |
|
А1 А2 А3 А4 |
20 75 25 85 |
30 20 80 5 |
15 25 35 45 |
15 20 25 5 |
30 75 80 85 |
21 42 47 37 |


По критерию Вальда оптимальной является стратегия A1, по критерию Гурвица с

Таблица 28.9
 Ai |
П1 |
П2 |
П3 |
П4 |
?i |
 |
hi |
|
А1 А2 А3 |
19 51 73 |
30 38 18 |
41 10 81 |
49 20 11 |
19 10 11 |
49 51 81 |
31 26 38 |
Минимальным в последнем столбце является число 38, так что критерий Сэвиджа, так же как и критерий Гурвица, «голосует» за стратегию А3.
Над этим стоит поразмыслить. Если мы очень боимся малого выигрыша «11», который нас может постигнуть при стратегии А3, ну что же — выберем стратегию A1,
рекомендуемую крайне осторожным критерием Вальда, при котором мы, по крайней мере, можем себе гарантировать выигрыш «19», а может быть, и больше. Если же наш пессимизм не так уж мрачен, пожалуй, надо остановиться на стратегии А3, рекомендуемой двумя из трех критериев.
Таблица 28.10
 Ai |
П1 |
П2 |
П3 |
П4 |
?i |
|
А1 А2 А3 |
54 22 0 |
8 0 20 |
40 71 0 |
0 29 38 |
54 71 38 |
В заключение отметим следующее: все три критерия (Вальда, Сэвиджа и Гурвица) были сформулированы нами для чистых стратегий, но каждый из них может быть распространен и на смешанные, подобно тому, как мы это делали в теории игр. Однако смешанные стратегии в игре с природой имеют лишь ограниченное (главным образом, теоретическое) значение. Если в игре против сознательного противника смешанные стратегии иногда имеют смысл как «трюк», вводящий в заблуждение противника, то в игре против «равнодушной природы» этот резон отпадает. Кроме того, смешанные стратегии приобретают смысл только при многократном повторении игры. А если уж мы ее повторяем, то неизбежно начинают вырисовываться какие-то вероятностные черты ситуации, и мы ими можем воспользоваться для того, чтобы применить «стохастический подход» к задаче, а он, как мы знаем, смешанных стратегий не дает. Кроме того, в ситуациях с «дурной» неопределенностью, когда нам мучительно не хватает информации, главная задача — эту информацию получить, а не выдумывать хитроумные методы, позволяющие без нее обойтись.
Одна из основных задач теории статистических решений — это как раз планирование эксперимента, цель которого — выяснение или уточнение каких-то данных. На вопросах планирования эксперимента мы здесь останавливаться не будем: это отдельный предмет, требующий серьезного внимания. По этому вопросу мы отошлем читателя к специальным руководствам [29, 30], а также к интересно написанной популярной книге [27]. Основной принцип теории планирования эксперимента состоит в том, что любое принятое заранее решение должно пересматриваться с учетом полученной новой информации,
* * *
Таким образом, наш краткий обзор, посвященный задачам, принципам и методологии исследования операции, закончен. В нем автор стремился ознакомить читателя не только с возможностями, но и с ограничениями математических методов, применяемых для обоснования решений. Главное — ни один из этих методов не избавляет человека от необходимости думать. Но не просто думать, а пользоваться при этом математическими расчетами. Помня, что, по меткому выражению Хемминга,— «главная цель расчетов — не цифры, а понимание».
