Преобразование определений
Конечно, построенное выше определение не отличается эффективностью. Обычно синтаксические формулы приводят к нормализованной форме, гарантирующей полезные свойства распознавателей и удобство их построения. Выбор нормализованной формы и процесс нормализации обосновывается доказательными построениями, на практике воспринимаемыми как эквивалентные преобразования. Преобразования формул — еще один интересный класс задач символьной обработки. Для демонстрации рассмотрим модель реализации функций свертки текстов. При подходящем выборе обозначений такие функции можно применять для преобразования синтаксических формул с целью приведения к нормализованной форме.
Пусть свертки системы текстов представлены в стиле самоописания подобно формам Бекуса-Наура списком вида:
( (Тексты (Имя Вариант ...)...) ; первое имя — обозначение системы текстов ; за ним следуют варианты поименованных текстов (Вариант Элемент ...) ; Вариант представляет собой ; последовательность Элементов (Элемент Имя Лексема (Варианты)) ; Элемент — это или Имя, или Лексема, ; или Варианты в скобках )
Для системы текстов «((м а ш и н а)(м а ш а)(ш и н а))» можно дать свертку вида:
( (пример (ма ((ш н) (ш а)) ( ш н ) ) (н ина) )
Построение свертки системы текстов выполняется функциями unic, ass-all, swin, gram, bnf :
(defun unic (vac) (remove-duplicates (mapcar 'car vac) )) ;; список уникальных начал
(defun ass-all (Key Vac) ;; список всех вариантов продолжения ;; что может идти за ключом (cond ((Null Vac) Nil) ((eq (caar Vac) Key) (cons (cdar Vac) (ass-all Key (cdr Vac)) )) (T (ass-all Key (cdr Vac)) ) ) )
(defun swin (key varl) (cond ;; очередной шаг свертки или снять скобки при ;; отсутствии вариантов ((null (cdr varl))(cons key (car varl))) (T (list key (gram varl)) ) ))
(defun gram (ltext) ;; левая свертка, если нашлись общие начала ( (lambda (lt) (cond ((eq (length lt)(length ltext)) ltext) (T (mapcar #'(lambda (k) (swin k (ass-all k ltext ) )) lt ) ) ) ) (unic ltext) ) )
(defun bnf (main ltext binds) (cons (cons main (gram ltext)) binds))
В результате синтаксические формулы можно приводить к нормализованному виду, пригодному для конструирования эффективного распознавателя с грамматикой текста. Организованные таким образом свернутые формы текстов могут играть роль словарей, грамматик языка, макетов программ и других древообразных структур данных, приспособленных к обработке рекурсивными функциями. обратные преобразования представляют не меньший интерес. Их можно использовать как генераторы тестов для синтаксических анализаторов или перечисления маршрутов в графе и других задач, решение которых сводится к обходу деревьев.
Построение развертки, т.е. системы текстов по их свернутому представлению, выполняется функциями names, words, lexs, d-lex, d-names, h-all, all-t, pred, sb-nm, chain, level1, lang.
Функции names, words и lexs задают алфавит и разбивают его на терминальные и нетерминальные символы на основе анализа их позиций в определении.
(defun names (vac) (mapcar 'car vac)) ;; определяемые символы
(defun words (vac) (cond ;; используемые символы ((null vac) NIL) ((atom vac) (cons vac NIL )) (T (union (words(car vac)) (words (cdr vac)))) ))
(defun lexs (vac) (set-difference (words vac) (names vac))) ;; неопределяемые лексемы
Функции d-lex и d-names формируют нечто вроде встроенной базы данных, хранящей определения символов для удобства дальнейшей работы.
(defun d-lex ( llex) ;; самоопределение терминалов (mapcar #'(lambda (x) (set x x) ) llex) )
(defun d-names ( llex) ;; определение нетерминалов (mapcar #'(lambda (x) (set (car x )(cdr x )) ) llex) )
Функции h-all, all-t и pred раскрывают слияния общих фрагментов системы текстов.
(defun h-all (h lt) ;; подстановка голов (mapcar #'(lambda (a) (cond ((atom h) (cons h a)) (T (append h a)) ) ) lt) ) (defun all-t (lt tl) ;; подстановка хвостов (mapcar #'(lambda (d) (cond ((atom d) (cons d tl)) (T(append d tl)) ) ) lt) )
(defun pred (bnf tl) ;; присоединение предшественников (level1 (mapcar #'(lambda (z) (chain z tl )) bnf) ))
Функции sb-nm, chain и LeveL1 строят развернутые, линейные тексты из частей, выполняя подстановку определений, сборку и выравнивание.
(defun sb-nm (elm tl) ;; подстановка определений имен (cond ((atom (eval elm)) (h-all (eval elm) tl)) (T (chain (eval elm) tl)) ) )
(defun chain (chl tl) ;; сборка цепочек (cond ((null chl) tl) ((atom chl) (sb-nm chl tl))
((atom (car chl)) (sb-nm (car chl) (chain (cdr chl) tl) ))
(T (pred (all-t (car chl) (cdr chl)) tl)) )) (defun level1 (ll) ;; выравниваие (cond ((null ll)NIL) (T (append (car ll) (level1 (cdr ll)) )) ))
На основе приведенных вспомогательных функций общая схема развертки языка по заданному его определению (свертке) может быть выполнена функцией lang:
(defun lang ( frm ) ;; вывод заданной системы текстов (d-lex (lexs frm)) (d-names frm) (pred (eval (caar frm)) '(()) ) )
Вот и тесты к этой задаче, предложенные И.Н. Скопиным, справедливо предположившим, что для решения задач синтаксически управляемой обработки текстов хорошо подходит функциональный стиль программирования на Лиспе:
(lang (print (bnf 'vars '((m a s h a)(m a s h i n a)(s h i n a)) '((n (i n a))) )))
(lang '((vars (m a ((s h a)(s h n))) (s h n) ) (n (i n a)) ) )
Цель преобразования синтаксических формул при определении анализаторов и компиляторов можно проиллюстрировать на схеме рекурсивного определения понятия «Идентификатор»:
Идентификатор ::= БУКВА | Идентификатор БУКВА | Идентификатор ЦИФРА
Удобное для эффективного синтаксического разбора определение имеет вид:
Идентификатор ::= БУКВА | БУКВА КонецИд
КонецИд ::= БУКВА КонецИд | ЦИФРА КонецИд | ПУСТО
Синтаксическая диаграмма анализатора
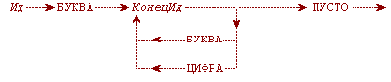
Рис. 13.1.
Этот пример показывает, что удобные для анализа формулы приведены к виду, когда каждую альтернативу можно выбрать по одному текущему символу. Система CLOS поддерживает ООП с выделением методов для одноэлементных классов, распознаваемых простым сравнением. Тем самым обеспечено удобное построение программ над структурами, подобными нормализованным формам.
Например, определение:
<а-гр> ::= А | А <а-гр>
<в-гр> ::= В | В <в-гр>
<слог> ::= <а-гр> <в-гр> | <в-гр> <а-гр> | <в-гр> <а-гр> <в-гр>
можно привести к виду, не требующему возвратов при анализе:
<а-гр> ::= А <а-кон> <а-кон> ::= <пусто> | A <а-кон>
<в-гр> ::= B <в-кон> <в-кон> ::= <пусто> | B <в-кон>
<слог> ::= A <а-кон> B <в-кон> |B <в-кон> A <а-кон> <в-кон>
Если программирование сводит алгоритм решения задачи к программе из определенной последовательности шагов, то конструирование строит программу решения задачи из решений типовых вспомогательных задач. Для задачи реализации языка программирования ключевой (но не единственной) типовой задачей является определение реализуемого языка. Ее решение открывает возможности автоматизированного конструирования анализаторов и компиляторов. Автоматизацию конструирования системы программирования обеспечивают методы синтаксического управления обработкой информации и методы смешанных/частичных вычислений, позволяющие выводить определение компилятора программ из определения интерпретатора.
Все это хорошо изученные задачи, имеющие надежные решения, знания которых достаточно для создания своих языков программирования и проведения экспериментов с программами на своих языках. Существует ряд программных инструментов, поддерживающих автоматизацию процесса создания и реализации языков программирования и более общих информационных систем обработки формализованной информации, например YACC, LEX, Bison, Flex, основные идеи применения которых достаточно близки изложенным выше методам обработки формул и текстов. Очередной этап в этом направлении открывают технологии типа .Net и DotGNU.

